题目内容
填空（x﹣y）（x2+xy+y2）= ；（x﹣y）（x3+x2y+xy2+y3）=
根据以上等式进行猜想，当n是偶数时，可得：（x﹣y）（xn+xn﹣1y+yn﹣2y2+…+x2yn﹣2+xyn﹣1+yn）= ．
根据以上等式进行猜想，当n是偶数时，可得：（x﹣y）（xn+xn﹣1y+yn﹣2y2+…+x2yn﹣2+xyn﹣1+yn）= ．
x3﹣y3 x4﹣y4 xn+1﹣yn+1
试题分析：根据多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．
解：原式=x3+x2y+xy2﹣x2y﹣xy2﹣y3=x3﹣y3；
故答案为：x3﹣y3；
原式=x4+x3y+x2y2+xy3﹣x3y﹣x2y2﹣xy3﹣y4=x4﹣y4；
故答案为：x4﹣y4；
原式=xn+1+xny+xyn﹣2+x2yn﹣1+xyn﹣xny﹣xn﹣1y2﹣yn﹣1y2﹣…﹣x2yn﹣1﹣xyn﹣yn+1=xn+1﹣yn+1，
故答案为：xn+1﹣yn+1．
点评：本题考查了多项式与多项式相乘的法则：多项式与多项式相乘，先用一个多项式的每一项乘另外一个多项式的每一项，再把所得的积相加．
练习册系列答案
相关题目
，
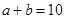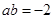，则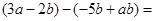
________