题目内容
【题目】如图,两个同心圆,大圆的弦AB与小圆相切于点P,大圆的弦CD经过点P,且CD=13,PD=4,则两圆组成的圆环的面积是( ) 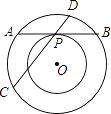
A.16π
B.36π
C.52π
D.81π
【答案】B
【解析】解:连接OP、OB. ∵大圆的弦AB与小圆相切于点P,
∴OP⊥AB,
∴PA=PB.
∵CD=13,PD=4,
∴PC=9.
根据相交弦定理,得PA=PB=6,
则两圆组成的圆环的面积是πOB2﹣πOP2=πPB2= ![]() AB2=36π.
AB2=36π.
故选B.
【考点精析】本题主要考查了相交弦定理和勾股定理的概念的相关知识点,需要掌握圆内的两条相交弦,被交点分成的两条线段长的积相等;如果弦与直径垂直相交,那么弦的一半是它分直径所成的两条线段的比例中项;直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2才能正确解答此题.

 阅读快车系列答案
阅读快车系列答案【题目】某班“数学兴趣小组”对函数y=x2﹣2|x|的图象和性质进行了探究.探究过程如下,请补充完整. 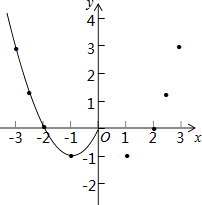
(1)自变量x的取值范围是全体实数,x与y的几组对应值列表:
x | … | ﹣3 | ﹣ | ﹣2 | ﹣1 | 0 | 1 | 2 |
| 3 | … |
y | … | 3 |
| m | ﹣1 | 0 | ﹣1 | n |
| 3 | … |
其中,m= , n= .
(2)根据表格数据,在如图所示的平面直角坐标系中描点,并画出了函数图象的一部分,请画出该图象的另一部分.
(3)观察函数图象,写出两条函数的性质:①;② .
(4)进一步探究函数图象发现: ①函数图象与x轴有个交点,所以对应的方程x2﹣2|x|=0有个实数根;
②方程x2﹣2|x|=2有个实数根.
【题目】某工艺品厂设计了一款成本为10元/件的小工艺品投放市场进行试销,经过调查,得到如下数据:
销售单价x(元/件) | … | 20 | 30 | 40 | 50 | 60 | … |
每天销售量y(件) | … | 500 | 400 | 300 | 200 | 100 | … |

(1)把上表中x,y的各组对应值作为点的坐标,在下面的平面直角坐标系中描出相应的点,猜想y与x的函数关系,并求出函数关系式.
(2)当销售单价为多少元时,工艺品厂试销该小工艺品每天获得的利润最大?最大利润是多少?(利润=销售额﹣成本)