题目内容
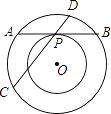
【题目】如图所示,⊙M与x轴相切于原点,平行于y轴的直线交圆于P,Q两点,P点在Q点的下方,若P点坐标是(2,1),则圆心M的坐标是( )
A.(0,3)
B.(0,2)
C.(0,![]() )
)
D.(0,![]() )
)
【答案】C
【解析】连接MP,过M作MA⊥PQ于A,设⊙M的半径为R,所以MP=R,PA=R-1,MA=PB=2,根据勾股定理则有:MP2=MA2+PA2 , 即可求得 R=![]() .
.
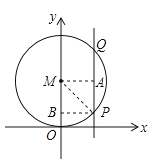
连MP,过M作MA⊥PQ于A,则PB=MA=2,
设⊙M的半径为R,则MP2=MA2+PA2 ,
即R2=22+(R-1)2 ,
解得R=![]() ,
,
故选:C.
【考点精析】关于本题考查的勾股定理的概念和垂径定理,需要了解直角三角形两直角边a、b的平方和等于斜边c的平方,即;a2+b2=c2;垂径定理:平分弦(不是直径)的直径垂直于弦,并且平分弦所对的两条弧才能得出正确答案.

练习册系列答案
相关题目