��Ŀ����
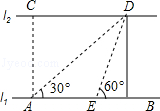
����Ŀ����ͼ����֪������y=��x2+9�Ķ���ΪA������DE��˫����y= ![]() ��3��x��12����һ���֣�����G1 �� ��D��3��m����E��12��m��3������������y=��x2+9ˮƽ�����ƶ�a����λ���õ�������G2 ��
��3��x��12����һ���֣�����G1 �� ��D��3��m����E��12��m��3������������y=��x2+9ˮƽ�����ƶ�a����λ���õ�������G2 �� 
��1����˫���ߵĽ���ʽ��
��2����������y=��x2+9��x��Ľ���ΪB��C����B��C����࣬���߶�BD�ij�Ϊ��
��3���㣨6��n��ΪG1��G2�Ľ������꣬��a��ֵ��
��4���⣺���ƶ������У���G1��G2���������㣬��G2�ĶԳ���ֱ��߶�DE��G1��M��N���㣬��MN�� ![]() ��ֱ��д��a��ȡֵ��Χ��
��ֱ��д��a��ȡֵ��Χ��
���𰸡�
��1��
��D��3��m����E��12��m��3������y= ![]() ��
�� 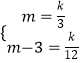 �����
����� ![]() ��
��
����˫���ߵĽ���ʽΪy= ![]() ��
��
��2��2 ![]()
��3��
�⣺�ѣ�6��n������y= ![]() ��6n=12�����n=2������������Ϊ��6��2����
��6n=12�����n=2��������������6��2����
������G2�Ľ���ʽΪy=����x��a��2+9��
�ѣ�6��2������y=����x��a��2+9�é���6��a��2+9=2�����a=6�� ![]() ��
��
��a��ֵΪ6�� ![]() ��
��
��4��
������G2�Ľ���ʽΪy=����x��a��2+9��
��D��3��4������y=����x��a��2+9���3��a��2+9=4�����a=3�� ![]() ��a=3+
��a=3+ ![]() ��
��
��E��12��1������y=����x��a��2+9���12��a��2+9=1�����a=12��2 ![]() ��a=12+2
��a=12+2 ![]() ��
��
��G1��G2���������㣬
��3+ ![]() ��a��12��2
��a��12��2 ![]() ��
��
��ֱ��DE�Ľ���ʽΪy=px+q��
��D��3��4����E��12��1������� ![]() �����
����� 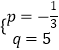 ��
��
��ֱ��DE�Ľ���ʽΪy=�� ![]() x+5��
x+5��
��G2�ĶԳ���ֱ��߶�DE��G1��M��N���㣬
��M��a���� ![]() a+5����N��a��
a+5����N��a�� ![]() ����
����
��MN�� ![]() ��
��
�ੁ ![]() a+5��
a+5�� ![]() ��
�� ![]() ��
��
������a2��13a+36��0������a��4����a��9����0��
��a��4��a��9��
��a��ȡֵ��ΧΪ9��a��12��2 ![]() ��
��
���������⣺��2����y=0ʱ����x2+9=0�����x1=��3��x2=3����B����3��0����
��D��3��4����
����BE= ![]() =2
=2 ![]() ��
��
���Դ���2 ![]() ��
��
�����㾫�������ڱ��⿼���ȷ��һ�κ����ı���ʽ�������ľ��룬��Ҫ�˽�ȷ��һ��һ�κ�������Ҫȷ��һ�κ�������ʽy=kx+b��k������0���еij���k��b�������������һ�㷽���Ǵ���ϵ������ͬ����������룬���С����Ϊ֮������Ⱦ������㣬���������ˣ�ƽ�����������㣬���ݱ������ֵ�����ӿ�ƽ�������빫ʽҪ�μDz��ܵó���ȷ�𰸣�

 һ����������ϵ�д�
һ����������ϵ�д�