题目内容
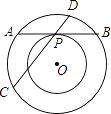
【题目】如图，已知四边形ABCD内接于圆O，连结BD，∠BAD=105°，∠DBC=75°．
（1）求证：BD=CD；
（2）若圆O的半径为3，求 
的长．
【答案】
（1）证明：∵四边形ABCD内接于圆O，
∴∠DCB+∠BAD=180°，
∵∠BAD=105°，
∴∠DCB=180°﹣105°=75°，
∵∠DBC=75°，
∴∠DCB=∠DBC=75°，
∴BD=CD；
（2）解：∵∠DCB=∠DBC=75°，
∴∠BDC=30°，
由圆周角定理，得， 
的度数为：60°，
故 = 
= 
=π，
答： 的长为π．
【解析】此题主要考查了弧长公式应用以及圆周角定理等知识，根据题意得出∠DCB的度数是解题关键．（1）直接利用圆周角定理得出∠DCB的度数，再利用∠DCB=∠DBC求出答案；（2）首先求出 的度数，再利用弧长公式直接求出答案．
练习册系列答案
相关题目
