Question

【题目】如图，△ABC中，D是BC上一点，∠DAC=∠B，E为AB上一点．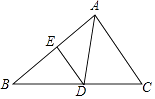
（1）求证：△CAD∽△CBA；
（2）若BD=10，DC=8，求AC的长；
（3）在（2）的条件下，若DE∥AC，AE=4，求BE的长．

Answer 1

【答案】
（1）解：∵在△CAD和△CBA中，

∠DAC=∠B，∠ACD=∠BCA，

∴△CAD∽△CBA

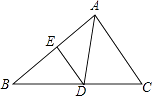
（2）解：∵△CAD∽△CBA，

∴ = ，即AC2=CD×CB，

又∵BD=10，DC=8，

∴AC2=8×18=144，

∴AC=±12，

又∵AC＞0，

∴AC=12

（3）解：∵DE∥AC，

∴ = ，

又∵BD=10，DC=8，AE=4，

∴ = ，

∴BE=5．

【解析】（1）有两组角对应相等的两个三角形相似，据此判断△CAD∽△CBA即可；（2）根据相似三角形的对应边成比例，得出AC2=CD×CB，再根据BD=10，DC=8，求得AC的长即可；（3）根据平行线分线段成比例定理，由DE∥AC，得出 = ，再根据BD=10，DC=8，AE=4，求得BE=5即可．
【考点精析】关于本题考查的平行线分线段成比例和相似三角形的判定与性质，需要了解三条平行线截两条直线，所得的对应线段成比例；相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等）的比等于相似比；相似三角形周长的比等于相似比；相似三角形面积的比等于相似比的平方才能得出正确答案．