题目内容
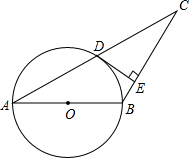
如图,在直角梯形ABCD中,AB∥CD,∠B=90°,AB=AD,∠BAD的平分线交BC于E,连接DE.
(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.

(1)说明点D在△ABE的外接圆上;
(2)若∠AED=∠CED,试判断直线CD与△ABE外接圆的位置关系,并说明理由.

证明:(1)证法一:∵∠B=90°,
∴AE是△ABE外接圆的直径.
取AE的中点O,则O为圆心,连接OB、OD.
在△AOB和△AOD中,
,
∴△AOB≌△AOD.
∴OD=OB.
∴点D在△ABE的外接圆上.
证法二:∵∠B=90°,
∴AE是△ABE外接圆的直径.
在△ABE和△ADE中,
,
∴△ABE≌△ADE.
∴∠ADE=∠B=90°.
取AE的中点O,则O为圆心,连接OD,则OD=
AE.
∴点D在△ABE的外接圆上.
(2)证法一:直线CD与△ABE的外接圆相切.
理由:∵AB∥CD,∠B=90度.∴∠C=90°.
∴∠CED+∠CDE=90°.
又∵OE=OD,
∴∠ODE=∠OED.
又∠AED=∠CED,
∴∠ODE=∠DEC.
∴∠ODC=∠CDE+∠ODE=∠CDE+∠CED=90°.
∴CD与△ABE的外接圆相切.
证法二:直线CD与△ABE的外接圆相切.
理由:∵AB∥CD,∠B=90度.∴∠C=90°.
又∵OE=OD,
∴∠ODE=∠OED.
又∠AED=∠CED,
∴∠ODE=∠DEC.
∴OD∥BC.
∴∠ODC=90°.
∴CD与△ABE的外接圆相切.
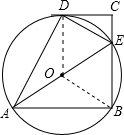
∴AE是△ABE外接圆的直径.
取AE的中点O,则O为圆心,连接OB、OD.
在△AOB和△AOD中,
|
∴△AOB≌△AOD.
∴OD=OB.
∴点D在△ABE的外接圆上.
证法二:∵∠B=90°,
∴AE是△ABE外接圆的直径.
在△ABE和△ADE中,
|
∴△ABE≌△ADE.
∴∠ADE=∠B=90°.
取AE的中点O,则O为圆心,连接OD,则OD=
| 1 |
| 2 |
∴点D在△ABE的外接圆上.
(2)证法一:直线CD与△ABE的外接圆相切.
理由:∵AB∥CD,∠B=90度.∴∠C=90°.
∴∠CED+∠CDE=90°.
又∵OE=OD,
∴∠ODE=∠OED.
又∠AED=∠CED,
∴∠ODE=∠DEC.
∴∠ODC=∠CDE+∠ODE=∠CDE+∠CED=90°.
∴CD与△ABE的外接圆相切.
证法二:直线CD与△ABE的外接圆相切.
理由:∵AB∥CD,∠B=90度.∴∠C=90°.
又∵OE=OD,
∴∠ODE=∠OED.
又∠AED=∠CED,
∴∠ODE=∠DEC.
∴OD∥BC.
∴∠ODC=90°.
∴CD与△ABE的外接圆相切.


练习册系列答案
相关题目