题目内容
已知：如图，△ABC中，以AB为直径的⊙O交AC于点D，且D为AC的中点，过D作DE丄CB，垂足为E．
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）已知CD=4，CE=3，求⊙O的半径．
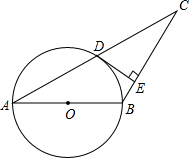
（1）判断直线DE与⊙O的位置关系，并说明理由；
（2）已知CD=4，CE=3，求⊙O的半径．
（1）证明：连接OD，
∵D为AC的中点，O为AB的中点，
∴DO∥BC，
∵DE丄CB，
∴DE⊥OD，
∴∠ODE=90°，
∴直线DE是⊙O的切线；
（2）连接BD，
∵AB是⊙O的直径，
∴∠ADB=90°，
∴BD⊥AC，
∴∠BDC=90°，
又∵DE⊥BC，
Rt△CDB∽Rt△CED，
∴
=
，
∴BC=
=
=
，
又∵OD=
BC，
∴OD=
×
=
，
即⊙O的半径为
．
∵D为AC的中点，O为AB的中点，
∴DO∥BC，
∵DE丄CB，
∴DE⊥OD，
∴∠ODE=90°，
∴直线DE是⊙O的切线；
（2）连接BD，
∵AB是⊙O的直径，
∴∠ADB=90°，
∴BD⊥AC，
∴∠BDC=90°，
又∵DE⊥BC，
Rt△CDB∽Rt△CED，
∴
| BC |
| DC |
| DC |
| CE |
∴BC=
| DC2 |
| CE |
| 42 |
| 3 |
| 16 |
| 3 |
又∵OD=
| 1 |
| 2 |
∴OD=
| 1 |
| 2 |
| 16 |
| 3 |
| 8 |
| 3 |
即⊙O的半径为
| 8 |
| 3 |
练习册系列答案
相关题目
，连接BO、ED，有BO
