题目内容
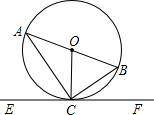
如图,O是已知线段AB上一点,以OB为半径的⊙O交线段AB于点C,以线段AO为直径的半圆交⊙O于点D,过点B作AB的垂线与AD的延长线交于点E;
(1)求证:AE切⊙O于点D;
(2)若AC=2,且AC、AD的长是关于x的方程x2-kx+4
=0的两根,求线段EB的长.

(1)求证:AE切⊙O于点D;
(2)若AC=2,且AC、AD的长是关于x的方程x2-kx+4
| 5 |

(1)证明:连接OD.
∵AO为半圆直径,∴∠ADO=90°.
∴AE切⊙O于点D;
(2)∵AC、AD的长是关于x的方程x2-kx+4
=0的两根,
∴AC•AD=4
;
∵AC=2,
∴AD=2
.
设OD=OC=x,则(x+2)2=(2
)2+x2.
解得x=4.
∴AB=2+8=10.
∵∠ADO=∠ABE=90°,∠A=∠A,
∴△AOD∽△AEB,
∴
=
,即
=
,
∴BE=4
.

∵AO为半圆直径,∴∠ADO=90°.
∴AE切⊙O于点D;
(2)∵AC、AD的长是关于x的方程x2-kx+4
| 5 |
∴AC•AD=4
| 5 |
∵AC=2,
∴AD=2
| 5 |
设OD=OC=x,则(x+2)2=(2
| 5 |
解得x=4.
∴AB=2+8=10.
∵∠ADO=∠ABE=90°,∠A=∠A,
∴△AOD∽△AEB,
∴
| OD |
| BE |
| AD |
| AB |
| 4 |
| BE |
2
| ||
| 10 |
∴BE=4
| 5 |


练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
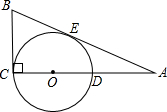



 C,垂足为点F.
C,垂足为点F. ,连接BO、ED,有BO
,连接BO、ED,有BO