题目内容
【题目】聪聪是一位非常喜欢动脑筋的初一学生，特别是学了几何后，更觉得数学奇妙，当聪聪学完
图形的初步知识
后对角平分线兴趣更浓厚，下面请你和聪聪同学一起来探究奇妙的角平分线吧
已知
，射线OE，OF分别是
和
的角平分线．
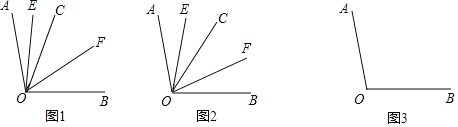
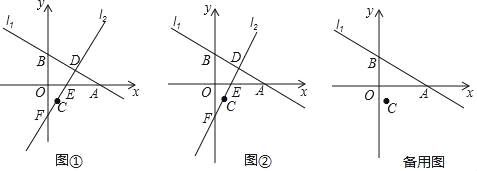
如图1，若射线OC在
的内部，且
，求
的度数；
如图2，若射线OC在的内部绕点O旋转，且
，求的度数；
若射线OC在的外部绕点O旋转
旋转中，
均指小于
的角
，其余条件不变，请借助图3探究
的大小，请直接写出的度数不写探究过程
【答案】（1）
；（2）50°；（3）
或
．
【解析】
先求出
度数，根据角平分线定义求出
和
度数，求和即可得出答案；
先求出度数，根据角平分线定义求出和度数，求和即可得出答案；
分两种情况：
射线OE，OF只有1个在
外面，根据角平分线定义得出
，
，求出
；
射线OE，OF2个都在外面，根据角平分线定义得出
，，求出
，代入求出即可．
解：
，
，
，
，OF分别是
和
的角平分线，
，
，
；
，
，
，
，OF分别是和的角平分线，
，
，
；
故答案为：．
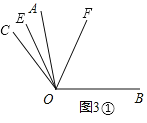
射线OE，OF只有1个在外面，如图
，
．
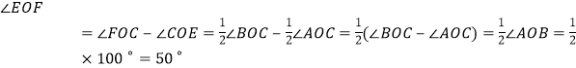射线OE，OF2个都在外面，如图
，
．
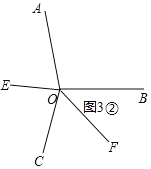
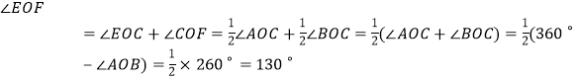故
的度数是或．
练习册系列答案
相关题目
