题目内容
【题目】在平面直角坐标系xOy中,直线l1:y=k1x+2![]() 与x轴、y轴分别交于点A、B两点,OA=
与x轴、y轴分别交于点A、B两点,OA=![]() OB,直线l2:y=k2x+b经过点C(1,﹣
OB,直线l2:y=k2x+b经过点C(1,﹣![]() ),与x轴、y轴和线段AB分别交于点E、F、D三点.
),与x轴、y轴和线段AB分别交于点E、F、D三点.
(1)求直线l1的解析式;
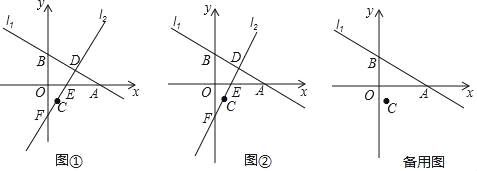
(2)如图①:若EC=ED,求点D的坐标和△BFD的面积;
(3)如图②:在坐标轴上是否存在点P,使△PCD是以CD为底边的等腰直角三角形,若存在,请直接写出点P的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)D(3,
;(2)D(3,![]() ),面积为6
),面积为6![]() ;(3)存在,满足条件的点P坐标为(0,4
;(3)存在,满足条件的点P坐标为(0,4![]() ﹣6)或(2
﹣6)或(2![]() ,0),理由见解析
,0),理由见解析
【解析】
(1)求出点A的坐标,利用待定系数法即可解决问题;
(2)如图1中,作CM⊥OA于M,DN⊥CA于N.由△CME≌△DNE(AAS),推出CM=DN由C(1,﹣![]() ),可得CM=DN=
),可得CM=DN=![]() ,再利用待定系数法即可解决问题;
,再利用待定系数法即可解决问题;
(3)分点P在y轴或x轴两种情形分别求解即可解决问题;
解:(1)∵直线y=k1x+2![]() 与y轴B点,
与y轴B点,
∴B(0,2![]() ),
),
∴OB=2![]() ,
,
∵OA=![]() OB=6,
OB=6,
∴A(6,0),
把A(6,0)代入y=k1x+2![]() 得到,k1=﹣
得到,k1=﹣![]() ,
,
∴直线l1的解析式为y=﹣![]() x+2
x+2![]() .
.
(2)如图1中,作CM⊥OA于M,DN⊥CA于N.
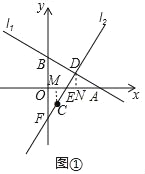
∵∠CME=∠DNE=90°,∠MEC=∠NED,EC=DE,
∴△CME≌△DNE(AAS),
∴CM=DN
∵C(1,﹣![]() ),
),
∴CM=DN=![]() ,
,
当y=![]() 时,
时,![]() =﹣
=﹣![]() x+2
x+2![]() ,
,
解得x=3,
∴D(3,![]() ),
),
把C(1,﹣![]() ),D(3,
),D(3,![]() )代入y=k2x+b,得到
)代入y=k2x+b,得到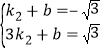 ,
,
解得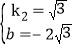 ,
,
∴直线CD的解析式为y=![]() x﹣2
x﹣2![]() ,
,
∴F(0,﹣2![]() ),
),
∴S△BFD=![]() ×4
×4![]() ×3=6
×3=6![]() .
.
(3)①如图③﹣1中,当PC=PD,∠CPD=90°时,作DM⊥OB于M,CN⊥y轴于N.设P(0,m).
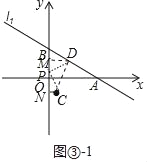
∵∠DMP=∠CNP=∠CPD=90°,
∴∠CPN+∠PCN=90°,∠CPN+∠DPM=90°,
∴∠PCN=∠DPM,
∵PD=PC,
∴△DMP≌△NPC(AAS),
∴CN=PM=1,PN=DM=m+![]() ,
,
∴D(m+![]() ,m+1),
,m+1),
把D点坐标代入y=﹣![]() x+2
x+2![]() ,得到:m+1=﹣
,得到:m+1=﹣![]() (m+
(m+![]() )+2
)+2![]() ,
,
解得m=4![]() ﹣6,
﹣6,
∴P(0,4![]() ﹣6).
﹣6).
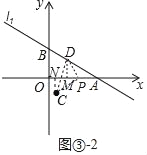
②如图③﹣2中,当PC=PC,∠CPD=90时,作DM⊥OA于M,CN⊥OA于N.设P(n,0).
同法可证:△AMD≌△PNC,
∴PM=CN=![]() ,DM=PN=n﹣1,
,DM=PN=n﹣1,
∴D(n﹣![]() ,n﹣1),
,n﹣1),
把D点坐标代入y=﹣![]() x+2
x+2![]() ,得到:n﹣1=﹣
,得到:n﹣1=﹣![]() (n﹣
(n﹣![]() )+2
)+2![]() ,
,
解得n=2![]()
∴P(2![]() ,0).
,0).
综上所述,满足条件的点P坐标为(0,4![]() ﹣6)或(2
﹣6)或(2![]() ,0)
,0)

【题目】小李在某商场购买![]() 两种商品若干次(每次
两种商品若干次(每次![]() 商品都买) ,其中前两次均按标价购买,第三次购买时,
商品都买) ,其中前两次均按标价购买,第三次购买时,![]() 商品同时打折.三次购买
商品同时打折.三次购买![]() 商品的数量和费用如下表所示:
商品的数量和费用如下表所示:
购买A商品的数量/个 | 购买B商品的数量/个 | 购买总费用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
(1)求![]() 商品的标价各是多少元?
商品的标价各是多少元?
(2)若小李第三次购买时![]() 商品的折扣相同,则商场是打几折出售这两种商品的?
商品的折扣相同,则商场是打几折出售这两种商品的?
(3)在(2)的条件下,若小李第四次购买![]() 商品共花去了
商品共花去了![]() 元,则小李的购买方案可能有哪几种?
元,则小李的购买方案可能有哪几种?