��Ŀ����
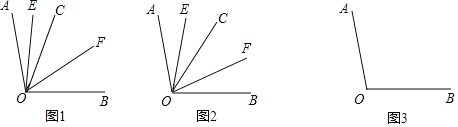
����Ŀ����ͼ1����֪��BAD����BCE��Ϊ����ֱ�������Σ���BAD=��BCE=90������MΪDE���е㣮����E��ADƽ�е�ֱ�߽�����AM�ڵ�N��
��1����A��B��C������ͬһֱ����ʱ����ͼ1������֤��MΪAN���е㣻
��2����ͼ1����BCE�Ƶ�B��ת����A��B��E������ͬһֱ����ʱ����ͼ2������֤����CANΪ����ֱ�������Σ�
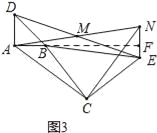
��3����ͼ1����BCE�Ƶ�B��ת��ͼ3��λ��ʱ��(2)�еĽ����Ƿ���Ȼ����������������֤��֮��������������˵�����ɣ�
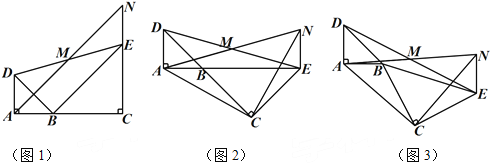
���𰸡���1��֤������������2��֤������������3����ACN��Ϊ����ֱ�������Σ�֤����������
�������������������1����EN��AD�͵�MΪDE���е����֤����ADM�ա�NEM���Ӷ�֤��MΪAN���е㣮
��2����֤AB=DA=NE����ABC=��NEC=135�����Ӷ�����֤����ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90����������ACNΪ����ֱ�������Σ�
��3���ӳ�AB��NE�ڵ�F������ADM�ա�NEM�������ı���BCEF�ڽǺͣ��ɵ���ABC=��FEC���Ӷ�����֤����ABC�ա�NEC����������֤��AC=NC����ACN=��BCE=90����������ACNΪ����ֱ�������Σ�
�����������1����ͼ1��
��EN��AD��
���MAD=��MNE����ADM=��NEM��
����MΪDE���е㣬
��DM=EM��
����ADM����NEM��
��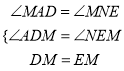 ��
��
���ADM�ա�NEM��
��AM=MN��
��MΪAN���е㣮
��2����ͼ2��
�ߡ�BAD����BCE��Ϊ����ֱ�������Σ�
��AB=AD��CB=CE����CBE=��CEB=45����
��AD��NE��
���DAE+��NEA=180����
�ߡ�DAE=90����
���NEA=90����
���NEC=135����
��A��B��E������ͬһֱ���ϣ�
���ABC=180�㩁��CBE=135����
���ABC=��NEC��
�ߡ�ADM�ա�NEM����֤����
��AD=NE��
��AD=AB��
��AB=NE��
����ABC����NEC��
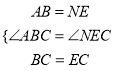
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90����
���ACNΪ����ֱ�������Σ�
��3����ACN��Ϊ����ֱ�������Σ�
֤������ͼ3���ӳ�AB��NE�ڵ�F��
��AD��NE��MΪ�е㣬
������ADM�ա�NEM��
��AD=NE��
��AD=AB��
��AB=NE��
��AD��NE��
��AF��NE��
���ı���BCEF�У�
�ߡ�BCE=��BFE=90��
���FBC+��FEC=360�㩁180��=180��
�ߡ�FBC+��ABC=180��
���ABC=��FEC
����ABC����NEC��
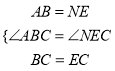
���ABC�ա�NEC��
��AC=NC����ACB=��NCE��
���ACN=��BCE=90����
���ACNΪ����ֱ�������Σ�

 ��������һ���þ�ϵ�д�
��������һ���þ�ϵ�д� Сѧ��10����Ӧ����ϵ�д�
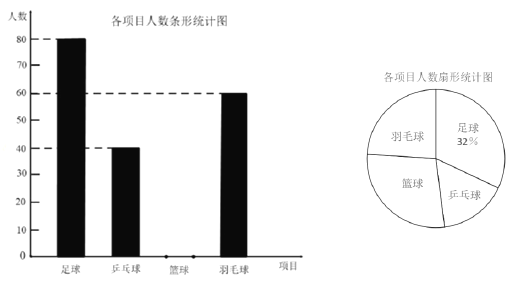
Сѧ��10����Ӧ����ϵ�д�����Ŀ��Ϊ�˹��������Լ��ˮ�����о���ʹ������ˮ�Ʒѷ�ʽʵʩ����ˮ�ۣ����������1����2�ֱ���С����С����С��С���ļ�2017�������ˮ���ͽ���ˮ�������
��1�������о�������ˮʵʩ����ˮ�۱������
���� | ÿ������ˮ���������ף� | ˮ�ۣ�����ˮ�����ѣ���Ԫ/�����ף� |
��һ���� | 0��m����m�� | a |
�ڶ����� | m��240����240�� | 4.40 |
�������� | 240���� | 7.85 |
��2���ĸ���ͥ2017�������ˮ���ͽ���ˮ�������
��ͥ | С�� | С�� | С�� | С�� |
��ˮ���������ף� | 50 | 100 | 200 | 220 |
ˮ�ѣ�Ԫ�� | 162.5 | 325 | 673 | 761 |
������ݱ�1����2�ṩ�����ݻش��������⣺
��1��д����1�е�a��m��ֵ��
��2��Сӱ��2017��ʹ������ˮ������ˮ��827Ԫ��������2017�������ˮ���Ƕ��������ף�