题目内容
【题目】已知，如图，∠BAE+∠AED=180°，∠1=∠2，那么∠M=∠N（下面是推理过程，请你填空）．
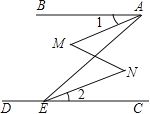
解：∵∠BAE+∠AED=180°（已知）
∴ ∥ （同旁内角互补，两直线平行）
∴∠BAE= （两直线平行，内错角相等）
又∵∠1=∠2
∴∠BAE﹣∠1= ﹣
即∠MAE=
∴ ∥ （内错角相等，两直线平行）
∴∠M=∠N（两直线平行，内错角相等）
【答案】AB，CD，∠AEC，∠AEC，∠2，∠AEN，AE，EN
【解析】
试题分析：由于∠BAE+∠AED=180°，根据平行线的判定定理可知AB∥CD，则∠BAE=∠AEC，因为∠1=∠2，可推出∠MAE=∠AEN，AM∥EN，∠M=∠N．
解：∵∠BAE+∠AED=180°（已知）
∴AB∥CD（同旁内角互补，两直线平行）
∴∠BAE=∠AEC（两直线平行，内错角相等）
又∵∠1=∠2
∴∠BAE﹣∠1=∠AEC﹣∠2
即∠MAE=∠AEN
∴AM∥EN（内错角相等，两直线平行）
∴∠M=∠N（两直线平行，内错角相等）．
【题目】为了鼓励市民节约用水，我市居民使用自来水计费方式实施阶梯水价，具体标准见表1，表2分别是小明、小丽、小斌、小宇四家2017年的年用水量和缴纳水费情况．
表1：大连市居民自来水实施阶梯水价标准情况：
阶梯 | 每户年用水量（立方米） | 水价（含污水处理费）（元/立方米） |
第一阶梯 | 0～m（含m） | a |
第二阶梯 | m～240（含240） | 4.40 |
第三阶梯 | 240以上 | 7.85 |
表2：四个家庭2017年的年用水量和缴纳水费情况：
家庭 | 小明 | 小丽 | 小斌 | 小宇 |
用水量（立方米） | 50 | 100 | 200 | 220 |
水费（元） | 162.5 | 325 | 673 | 761 |
请你根据表1、表2提供的数据回答下列问题：
（1）写出表1中的a，m的值；
（2）小颖家2017年使用自来水共缴纳水费827元，则她家2017年的年用水量是多少立方米？
【题目】小李在某商场购买
两种商品若干次(每次商品都买) ，其中前两次均按标价购买，第三次购买时，商品同时打折．三次购买商品的数量和费用如下表所示：
购买A商品的数量/个 | 购买B商品的数量/个 | 购买总费用/元 | |
第一次 |
|
|
|
第二次 |
|
|
|
第三次 |
|
|
|
（1）求
商品的标价各是多少元？
（2）若小李第三次购买时商品的折扣相同，则商场是打几折出售这两种商品的？
（3）在（2）的条件下，若小李第四次购买商品共花去了
元，则小李的购买方案可能有哪几种？
