ЬтФПФкШн
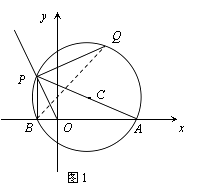
ЁОЬтФПЁПШчЭМЃЌдкжБНЧзјБъЯЕжаЕуAЃЈ2ЃЌ0ЃЉЃЌЕуPдкЩфЯп ![]() ЃЈxЃМ0ЃЉЩЯдЫЖЏЃЌЩшЕуPЕФКсзјБъЮЊaЃЌвдAPЮЊжБОЖзїЁбCЃЌСЌНгOPЁЂPBЃЌЙ§ЕуPзїPQЁЭOPНЛЁбCгкЕуQЃЎ
ЃЈxЃМ0ЃЉЩЯдЫЖЏЃЌЩшЕуPЕФКсзјБъЮЊaЃЌвдAPЮЊжБОЖзїЁбCЃЌСЌНгOPЁЂPBЃЌЙ§ЕуPзїPQЁЭOPНЛЁбCгкЕуQЃЎ
ЃЈ1ЃЉжЄУїЃКЁЯAOP=ЁЯBPQЃЛ
ЃЈ2ЃЉЕБЕуPдкдЫЖЏЕФЙ§ГЬжаЃЌЯпЖЮPQЕФГЄЖШЪЧЗёЗЂЩњБфЛЏЃЌШєБфЛЏЃЌЧыгУКЌaЕФДњЪ§ЪНБэЪОPQЕФГЄЃЛШєВЛБфЃЌЧѓГіPQЕФГЄЃЛ
ЃЈ3ЃЉЕБtanЁЯAPO= ![]() ЪБЃЌЂйЧѓЕуQзјБъЃЛЂкЕуDЪЧдВЩЯШЮвтвЛЕуЃЌЧѓQD+
ЪБЃЌЂйЧѓЕуQзјБъЃЛЂкЕуDЪЧдВЩЯШЮвтвЛЕуЃЌЧѓQD+ ![]() ODЕФзюаЁжЕЃЎ
ODЕФзюаЁжЕЃЎ
ЁОД№АИЁП
ЃЈ1ЃЉНтЃКгЩЬтвтЕУЕуPЃЈaЃЌЃ ![]() aЃЉЃЌЁпAPЮЊжБОЖЃЌЁрЁЯPBA=90ЁуЃЌЁрtanЁЯBOP=
aЃЉЃЌЁпAPЮЊжБОЖЃЌЁрЁЯPBA=90ЁуЃЌЁрtanЁЯBOP= ![]() ЃЌЁрЁЯBPO=30ЁуЃЌЁЯPOB=60ЁуЃЌЁпPQЁЭOPЃЌЁрЁЯBPQ=ЁЯAOP=120Ёу
ЃЌЁрЁЯBPO=30ЁуЃЌЁЯPOB=60ЁуЃЌЁпPQЁЭOPЃЌЁрЁЯBPQ=ЁЯAOP=120Ёу
ЃЈ2ЃЉНтЃКВЛБфЃЎШчЭМ1ЃЌСЌНсBQЃЌ
ЁпЁЯQ=ЁЯPAOЃЌЁЯBPQ=ЁЯAOPЃЌ
ЁрЁїBPQЁзЁїPOAЃЎ
Ёр ![]() ЃЌ
ЃЌ
ЁрPQ= ![]()
ЃЈ3ЃЉНтЃКЂйШчЭМ2ЃЌСЌНсAQЃЌЙ§ЕуQзїQHЁЭBP
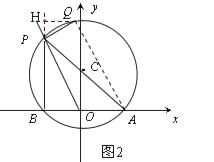
ЁпAPЪЧжБОЖЃЌ
ЁрЁЯPQA=90ЁуЃЎ
ЁпЁЯOPQ=90ЁуЃЌ
ЁрOPЁЮAQЃЎ
ЁрЁЯOPA=ЁЯPAQЃЌ
ЁпtanЁЯOPA= ![]() ЃЌ
ЃЌ
Ёр ![]() ЃЌ
ЃЌ
ЁпPQ= ![]() ЃЌ
ЃЌ
ЁрAQ=5ЃЌAP=2 ![]() ЃЌдкRTЁїABPжаЃЌAB=2ЃaЃЌBP=Ѓ
ЃЌдкRTЁїABPжаЃЌAB=2ЃaЃЌBP=Ѓ ![]() aЃЌгЩЃЈ2-aЃЉ2+ЃЈ
aЃЌгЩЃЈ2-aЃЉ2+ЃЈ ![]() aЃЉ2=ЃЈ2
aЃЉ2=ЃЈ2 ![]() ЃЉ2ЃЌНтЕУa1=Ѓ2ЃЌa2=3ЃЈЩсШЅЃЉЃЌ
ЃЉ2ЃЌНтЕУa1=Ѓ2ЃЌa2=3ЃЈЩсШЅЃЉЃЌ
ЁрPЃЈЃ2ЃЌ2 ![]() ЃЉЃЌЁЯBPQ=120ЁуЃЌ
ЃЉЃЌЁЯBPQ=120ЁуЃЌ
ЁрЁЯHPQ=60ЁуЃЌ
ЁрPH= ![]() ЃЌHQ=
ЃЌHQ= ![]() ЃЌ
ЃЌ
ЁрЕуQЃЈ- ![]() ЃЌ
ЃЌ ![]() ЃЉЃЛ
ЃЉЃЛ
ЂкШчЭМ3ЃЌ
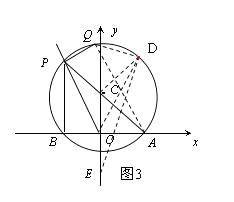
гЩЂйЕУCD= ![]() ЃЌ
ЃЌ
ЁпPЃЈЃ2ЃЌ2 ![]() ЃЉ,AЃЈ2ЃЌ0ЃЉЃЌ
ЃЉ,AЃЈ2ЃЌ0ЃЉЃЌ
ЁрCЃЈ0ЃЌ ![]() ЃЉ ,OC=
ЃЉ ,OC= ![]() ЃЌдкyжсЩЯевЕуEЪЙCE=
ЃЌдкyжсЩЯевЕуEЪЙCE= ![]() ЃЌ
ЃЌ
ЁрEЃЈ0ЃЌ- ![]() ЃЉЃЌ
ЃЉЃЌ
ЁрCD2=COЁЄCEЃЌ
ЁпЁЯDCO=ЁЯECDЃЌ
ЁрЁїDCOЁзЁїECDЃЌ
ЁрDE= ![]() ODЃЌ
ODЃЌ
ЁпQD+DEЁнQEЃЌ
ЁрQD+ ![]() ODЕФзюаЁжЕЮЊ
ODЕФзюаЁжЕЮЊ ![]()
ЁОНтЮіЁПЃЈ1ЃЉЪзЯШБэЪОГіPЕуЕФзјБъЃЌИљОнжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЕУГіЁЯPBA=90ЁуЃЌИљОне§ЧаШ§НЧКЏЪ§ЕФЖЈвхМАЬиЪтШёНЧШ§НЧКЏЪ§жЕЕУГіЁЯPOB=60ЁуЃЌИљОнШ§НЧаЮЕФФкНЧКЭЕУГіЁЯBPO=30ЁуЃЌдйИљОнДЙжБЕФЖЈвхЕУГіЁЯBPQ=ЁЯAOP=120ЁуЃЛ
ЃЈ2ЃЉВЛБфЃЎШчЭМ1ЃЌСЌНсBQЃЌИљОнЭЌЛЁЫљЖдЕФдВжмНЧЯрЕШЕУГіЁЯQ=ЁЯPAOЃЌгжгЩЃЈ1ЃЉжЊЁЯBPQ=ЁЯAOPЃЌДгЖјХаЖЯГіЁїBPQЁзЁїPOAЃЌИљОнЯрЫЦШ§НЧаЮЖдгІБпГЩБШР§ЕУГіД№АИЃЛ
ЃЈ3ЃЉЂйШчЭМ2ЃЌСЌНсAQЃЌЙ§ЕуQзїQHЁЭBPЃЌИљОнжБОЖЫљЖдЕФдВжмНЧЪЧжБНЧЕУГіЁЯPQA=90ЁуЃЌШЛКѓИљОнЭЌХдФкНЧЛЅВЙСНжБЯпЦНааЕУГіOPЁЮAQЃЌИљОнЦНааЯпЕФаджЪЕУГіЁЯOPA=ЁЯPAQЃЌШЛКѓИљОне§ЧаШ§НЧКЏЪ§ЕФЖЈвхДђЕУГі![]() =
=![]() ЃЌДгЖјЕУГіAQ,APЕФГЄЃЌдкRtЁїABPжа,ИљОнЙДЙЩЖЈРэЕУГіЙигкaЕФЗНГЬЃЌЧѓГіaЕФжЕЃЌДгЖјЕУГіpЕуЕФзјБъЃЌНјвЛВНЕУГіQЕуЕФзјБъЃЛЂкШчЭМ3ЃЌгЩЂйЕУCD=
ЃЌДгЖјЕУГіAQ,APЕФГЄЃЌдкRtЁїABPжа,ИљОнЙДЙЩЖЈРэЕУГіЙигкaЕФЗНГЬЃЌЧѓГіaЕФжЕЃЌДгЖјЕУГіpЕуЕФзјБъЃЌНјвЛВНЕУГіQЕуЕФзјБъЃЛЂкШчЭМ3ЃЌгЩЂйЕУCD= ![]() ЃЌгЩP,AСНЕуЕФзјБъЕУГіCЕуЕФзјБъМАOCЕФГЄЃЌдкyжсЩЯевЕуEЪЙCE=
ЃЌгЩP,AСНЕуЕФзјБъЕУГіCЕуЕФзјБъМАOCЕФГЄЃЌдкyжсЩЯевЕуEЪЙCE= ![]() ЃЌНјЖјЕУГіEЕузјБъЃЌДгЖјЕУГіCD2=COЁЄCEЃЌШЛКѓХаЖЯГіЁїDCOЁзЁїECDЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУГіDE=
ЃЌНјЖјЕУГіEЕузјБъЃЌДгЖјЕУГіCD2=COЁЄCEЃЌШЛКѓХаЖЯГіЁїDCOЁзЁїECDЃЌИљОнЯрЫЦШ§НЧаЮЕФаджЪЕУГіDE= ![]() ODЃЌгжвђQD+DEЁнQEЃЌДгЖјЕУГіД№АИЁЃ
ODЃЌгжвђQD+DEЁнQEЃЌДгЖјЕУГіД№АИЁЃ
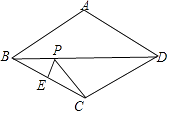
ЁОПМЕуОЋЮіЁПШЯецЩѓЬтЃЌЪзЯШашвЊСЫНтЦНааЯпЕФХаЖЈгыаджЪ(гЩНЧЕФЯрЕШЛђЛЅВЙЃЈЪ§СПЙиЯЕЃЉЕФЬѕМўЃЌЕУЕНСНЬѕжБЯпЦНааЃЈЮЛжУЙиЯЕЃЉетЪЧЦНааЯпЕФХаЖЈЃЛгЩЦНааЯпЃЈЮЛжУЙиЯЕЃЉЕУЕНгаЙиНЧЯрЕШЛђЛЅВЙЃЈЪ§СПЙиЯЕЃЉЕФНсТлЪЧЦНааЯпЕФаджЪ)ЃЌЛЙвЊеЦЮедВжмНЧЖЈРэ(ЖЅЕудкдВаФЩЯЕФНЧНазідВаФНЧ;ЖЅЕудкдВжмЩЯЃЌЧвЫќЕФСНБпЗжБ№гыдВгаСэвЛИіНЛЕуЕФНЧНазідВжмНЧ;вЛЬѕЛЁЫљЖдЕФдВжмНЧЕШгкЫќЫљЖдЕФдВаФНЧЕФвЛАы)ЕФЯрЙижЊЪЖВХЪЧД№ЬтЕФЙиМќЃЎ

ЁОЬтФПЁПШчЭМЃЌOMЦНЗжЁЯAOBЃЌMCЁЮOBЃЌMDЁЭOBгкDЃЌШєЁЯOMD=75ЁуЃЌOC=8ЃЌдђMDЕФГЄЮЊЃЈ ЃЉ

AЃЎ2 BЃЎ3 CЃЎ4 DЃЎ5
ЁОЬтФПЁПаЁРюдкФГЩЬГЁЙКТђ![]() СНжжЩЬЦЗШєИЩДЮ(УПДЮ
СНжжЩЬЦЗШєИЩДЮ(УПДЮ![]() ЩЬЦЗЖМТђ) ЃЌЦфжаЧАСНДЮОљАДБъМлЙКТђЃЌЕкШ§ДЮЙКТђЪБЃЌ
ЩЬЦЗЖМТђ) ЃЌЦфжаЧАСНДЮОљАДБъМлЙКТђЃЌЕкШ§ДЮЙКТђЪБЃЌ![]() ЩЬЦЗЭЌЪБДђелЃЎШ§ДЮЙКТђ
ЩЬЦЗЭЌЪБДђелЃЎШ§ДЮЙКТђ![]() ЩЬЦЗЕФЪ§СПКЭЗбгУШчЯТБэЫљЪОЃК
ЩЬЦЗЕФЪ§СПКЭЗбгУШчЯТБэЫљЪОЃК
ЙКТђAЩЬЦЗЕФЪ§СП/Иі | ЙКТђBЩЬЦЗЕФЪ§СП/Иі | ЙКТђзмЗбгУ/дЊ | |
ЕквЛДЮ |
|
|
|
ЕкЖўДЮ |
|
|
|
ЕкШ§ДЮ |
|
|
|
ЃЈ1ЃЉЧѓ![]() ЩЬЦЗЕФБъМлИїЪЧЖрЩйдЊЃП
ЩЬЦЗЕФБъМлИїЪЧЖрЩйдЊЃП
ЃЈ2ЃЉШєаЁРюЕкШ§ДЮЙКТђЪБ![]() ЩЬЦЗЕФелПлЯрЭЌЃЌдђЩЬГЁЪЧДђМИелГіЪлетСНжжЩЬЦЗЕФЃП
ЩЬЦЗЕФелПлЯрЭЌЃЌдђЩЬГЁЪЧДђМИелГіЪлетСНжжЩЬЦЗЕФЃП
ЃЈ3ЃЉдкЃЈ2ЃЉЕФЬѕМўЯТЃЌШєаЁРюЕкЫФДЮЙКТђ![]() ЩЬЦЗЙВЛЈШЅСЫ
ЩЬЦЗЙВЛЈШЅСЫ![]() дЊЃЌдђаЁРюЕФЙКТђЗНАИПЩФмгаФФМИжжЃП
дЊЃЌдђаЁРюЕФЙКТђЗНАИПЩФмгаФФМИжжЃП