题目内容
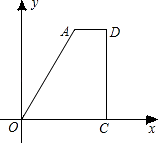
【题目】如图,在直角坐标系中,O为原点.点A在x轴的正半轴上,点B在y轴的正半轴上,tan∠OAB=2.二次函数y=x2+mx+2的图象经过点A,B,顶点为D.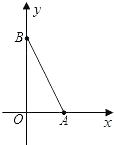
(1)求这个二次函数的解析式;
(2)将△OAB绕点A顺时针旋转90°后,点B落到点C的位置.将上述二次函数图象沿y轴向上或向下平移后经过点C.请直接写出点C的坐标和平移后所得图象的函数解析式;
(3)设(2)中平移后所得二次函数图象与y轴的交点为B1 , 顶点为D1 . 点P在平移后的二次函数图象上,且满足△PBB1的面积是△PDD1面积的2倍,求点P的坐标.
【答案】
(1)解:由题意,点B的坐标为(0,2),
∴OB=2,
∵tan∠OAB=2,即 ![]() =2.
=2.
∴OA=1.
∴点A的坐标为(1,0).
又∵二次函数y=x2+mx+2的图象过点A,
∴0=12+m+2.
解得m=﹣3,
∴所求二次函数的解析式为y=x2﹣3x+2
(2)解:作CE⊥x轴于E,
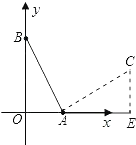
由于∠BAC=90°,可知∠CAE=∠OBA,△CAE≌△OBA,
可得CE=OA=1,AE=OB=2,可得点C的坐标为(3,1).
由于沿y轴运动,故图象开口大小、对称轴均不变,
设出解析式为y=x2﹣3x+c,代入C点作标得1=9﹣9+c,c=1,
所求二次函数解析式为y=x2﹣3x+1.
(3)解:由(2),经过平移后所得图象是原二次函数图象向下平移1个单位后所得的图象,
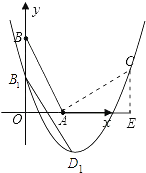
那么对称轴直线x= ![]() 不变,且BB1=DD1=1.
不变,且BB1=DD1=1.
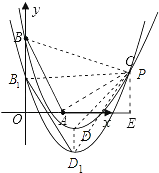
∵点P在平移后所得二次函数图象上,
设点P的坐标为(x,x2﹣3x+1).
在△PBB1和△PDD1中,∵S△PBB1=2S△PDD1,
∴边BB1上的高是边DD1上的高的2倍.
①当点P在对称轴的右侧时,x=2(x﹣ ![]() ),得x=3,
),得x=3,
∴点P的坐标为(3,1);
②当点P在对称轴的左侧,同时在y轴的右侧时,x=2( ![]() ﹣x),得x=1,
﹣x),得x=1,
∴点P的坐标为(1,﹣1);
③当点P在y轴的左侧时,x<0,又﹣x=2( ![]() ﹣x),
﹣x),
得x=3>0(舍去),
∴所求点P的坐标为(3,1)或(1,﹣1)
【解析】(1)二次函数y=x2+mx+2的图象经过点B,可得B点坐标为(0,2),再根据tan∠OAB=2求出A点坐标,将A代入解析式即可求得函数解析式;(2)根据旋转不变性可轻松求得C点坐标,由于沿y轴运动,故图象开口大小、对称轴均不变,设出解析式,代入C点作标即可求解;(3)由于P点位置不固定,由图可知要分①当点P在对称轴的右侧时,②当点P在对称轴的左侧,同时在y轴的右侧时,③当点P在y轴的左侧时,三种情况讨论.

 名校课堂系列答案
名校课堂系列答案