Question

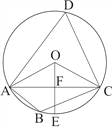
【题目】如图，四边形ABCD 是⊙O的内接四边形，∠ABC=2∠D,连接OA，OC,AC

（1）求∠OCA的度数 （2）如果OEAC于F,且OC=, 求AC的长

Answer 1

【答案】(1) 30°;(2)6

【解析】试题分析：（1）由圆内接四边形的性质得到∠ABC+∠D=180°，即可得到∠D的度数，再由圆周角定理得到∠AOC的度数，根据等腰三角形的性质即可得到∠OCA的度数；

（2）由30°角直角三角形三边关系可以得到OF，CF的长，再由垂径定理即可得到结论．

试题解析：解：（1）∵四边形ABCD 是⊙O的内接四边形，∴∠ABC+ ∠D=180°．

∵∠ABC=2∠D∴∠D+2∠D=180°，∴∠D=60°，∴∠AOC=2∠D=120°．

∵OA=OC，∴∠OCA=∠OAC=30°；

（2）在Rt△OCF中，OC=，∠OCA=30°， ∴OF=OC=，FC=OF=3．

∵OEAC， ∴AC=2CF=6．