题目内容
【题目】如图,在△ABC中,∠ACB=90°,CD平分∠ACB交AB于点D,将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上.
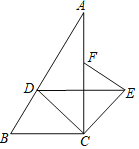
(1)△CDB旋转的度数;(2)连结DE,判断DE与BC的位置关系,并说明理由.
【答案】(1)△CDB旋转的度数:90°;(2)DE∥BC,见解析.
【解析】
(1)根据旋转的性质确定旋转角的度数;
(2)先利用旋转的性质得∠DCE=∠BCF=90°,CD=CE,则可判断△CDE为等腰直角三角形,所以∠CDE=45°,再利用角平分线定义得到∠BCD=45°,则∠CDE=∠BCD,然后根据平行线的判定方法可判断DE∥BC.
解:(1)∵将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上,
∴旋转角为∠BCF,
即旋转角为90°;
(2)DE∥BC.
理由如下:∵将△CDB绕点C顺时针旋转到△CEF的位置,点F在AC上,
∴∠DCE=∠BCF=90°,CD=CE,
∴△CDE为等腰直角三角形,
∴∠CDE=45°,
∵CD平分∠ACB交AB于点D,
∴∠BCD=45°,
∴∠CDE=∠BCD,
∴DE∥BC.

练习册系列答案
 全能测控期末小状元系列答案
全能测控期末小状元系列答案
相关题目