题目内容
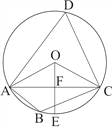
【题目】小红和小明在操场做游戏,他们先在地上画了半径分别2m和3m的同心圆(如图),蒙上眼在一定距离外向圈内掷小石子,掷中阴影小红胜,否则小明胜,未掷入圈内不算,你来当裁判.
(1)你认为游戏公平吗?为什么?
(2)游戏结束,小明边走边想,“反过来,能否用频率估计概率的方法,来估算某一不规则图形的面积呢”.请你设计方案,解决这一问题.(要求补充完整图形,说明设计步骤、原理,写出估算公式)

【答案】(1)不公平,理由详见解析;(2)详见解析.
【解析】试题分析:(1)分别计算出阴影部分面积和非阴影部分面积,小红胜的概率=S阴影÷S总,小明胜的概率=S非阴影÷S总,则比较阴影部分和小圆面积即可知道是否公平;(2)用一正方形将不规则图形包围起来,根据用频率估计概率来设计.
解:(1)不公平,理由:
根据几何概率的求法:掷中阴影小红胜的概率就是阴影区域的面积与总面积的比值;小明胜的概率为小圆面积与总面积的比值,
而计算可得大圆面积为9π,小圆面积为4π.则阴影部分面积为5π,
则阴影部分面积比小圆面积大.
则小红胜的概率大于小明胜的概率,
所以该游戏是不公平的,对小红有利;
(2)能利用频率估计概率的实验方法估算非规则图形的面积.
设计方案:①设计一个面积为S的正方形将非规则图形围起来,如图:
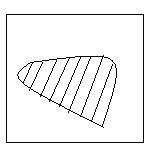
②蒙上眼在一定距离外向正方形内掷小石子,掷在正方形外不作记录;
③掷的次数充分大,记录并统计结果,其中掷入正方形内m次,n次掷非规则图形内;
④设非规则图形的面积为S1,用频率估计概率,即频率P(掷入非规则图形内)=![]() ≈概率P(掷入非规则图形内)=
≈概率P(掷入非规则图形内)=![]() ,解得S1≈
,解得S1≈![]() .
.

练习册系列答案
相关题目