题目内容
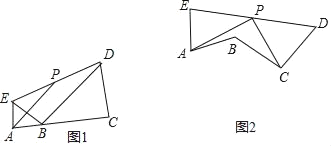
【题目】如图,四边形ABCD是平行四边形,F、G是AD边上的两个点,且FC平分∠BCD,GB平分∠ABC,FC与GB交于点E.
①AB=AG;②连接BF、CG,则四边形BFGC为等腰梯形;③AF=DG;④△ABG∽△DCF.
以上四个结论中一定成立的有( )个.

A. 1 B. 2 C. 3 D. 4
【答案】B
【解析】①∵GB平分∠ABC,
∴∠ABG=∠CBG,
在平行四边形ABCD中,AD∥BC,
∴∠CBG=∠AGB,
∴∠ABG=∠AGB,
∴AB=AG,故本小题正确;
②假设四边形BFGC为等腰梯形,则
BG=CF,
∴∠CBG=∠BCF,
又∵FC平分∠BCD,GB平分∠ABC,
∴∠ABC=2∠CBG,∠BCD=2∠BCF,
∴∠ABC=∠BCD,
由图可知,平行四边形ABCD的两邻角∠ABC和∠BCD不相等,故本小题错误;
③根据①AB=AG,
同理可得,CD=DF,
在平行四边形ABCD中,AB=CD,
∴AG=DF,
∴AG﹣GF=DF﹣GF,
即AF=DG,故本小题正确;
④由图可知,△ABG是钝角三角形,△DCF是锐角三角形,
所以△ABG和△DCF形状不同,不可能相似,故本小题错误,
综上所述,正确的是①③共2个.
故选B.

练习册系列答案
相关题目