题目内容
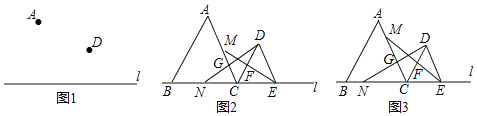
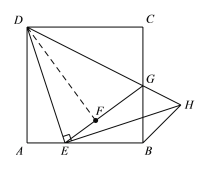
【题目】如图,在正方形ABCD中,E是边AB上的一动点(不与点A、B重合),连接DE,点A关于直线DE的对称点为F,连接EF并延长交BC于点G,连接DG,过点E作EH⊥DE交DG的延长线于点H,连接BH.
(1)求证:GF=GC;
(2)用等式表示线段BH与AE的数量关系,并证明.

【答案】(1)证明见解析;(2)BH=![]() AE,理由见解析.
AE,理由见解析.
【解析】
(1)连接![]() .根据对称的性质可得
.根据对称的性质可得![]() .
.![]() .证明
.证明![]() ,根据全等三角形的性质得到
,根据全等三角形的性质得到![]() .进而证明
.进而证明![]() ≌
≌![]() ,即可证明.
,即可证明.
(2)在![]() 上取点
上取点![]() 使得
使得![]() ,连接
,连接![]() .证明
.证明![]() ≌
≌![]() ,根据等腰直角三角形的性质即可得到线段
,根据等腰直角三角形的性质即可得到线段![]() 与
与![]() 的数量关系.
的数量关系.
(1)证明:连接![]() .
.
∵![]() ,
,![]() 关于
关于![]() 对称.
对称.
∴![]() .
.![]() .
.
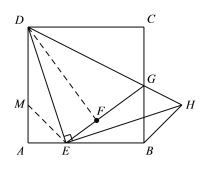
在![]() 和
和![]() 中.
中.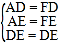
∴![]()
∴![]() .
.
∵四边形![]() 是正方形
是正方形
∴![]() .
.![]()
∴![]()
∴![]()
∴![]()
∵![]() .
.![]()
∴![]()
在![]() 和
和![]() .
.![]()
∴![]() ≌
≌![]()
∴![]() .
.
(2)![]() .
.
证明:在![]() 上取点
上取点![]() 使得
使得![]() ,连接
,连接![]() .
.
∵四这形![]() 是正方形.
是正方形.
∴![]() .
.![]() .
.
∵![]() ≌
≌![]()
∴![]()
同理:![]()
∴![]()
∵![]()
∴![]()
∴![]()
∴![]()
∴![]() .
.
∵![]()
∴![]()
∵![]()
∴![]()
∴![]()
∵![]() .
.![]()
∴![]()
在![]() 和
和![]() 中
中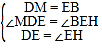
∴![]() ≌
≌![]()
∴![]()
在![]() 中,
中,![]() ,
,![]() .
.
∴![]()
∴![]() .
.

练习册系列答案
 快乐小博士巩固与提高系列答案
快乐小博士巩固与提高系列答案
相关题目
【题目】小明家买了一辆小轿车,小明连续记录了某一周每天行驶的路程:
星期一 | 星期二 | 星期三 | 星期四 | 星期五 | 星期六 | 星期日 | |
路程(千米) |
|
|
|
|
|
|
|
请你用学过的知识解决下面的问题:
(1)请你估计小明家的轿车每月(按![]() 天计算)要行驶多少千米?
天计算)要行驶多少千米?
(2)已知每行驶![]() 千米需汽油
千米需汽油![]() 升,汽油每升
升,汽油每升![]() 元,试用含
元,试用含![]() 、
、![]() 的代数式表示小明家每月的汽油费,此代数式为_______;
的代数式表示小明家每月的汽油费,此代数式为_______;
(3)设![]() ,
,![]() ,请你求出小明家一年(按
,请你求出小明家一年(按![]() 个月计算)的汽油费用大约是多少元(精确到千元).(注:第(1)、(3)小题须写出必要步骤)
个月计算)的汽油费用大约是多少元(精确到千元).(注:第(1)、(3)小题须写出必要步骤)