题目内容
【题目】综合与探究:
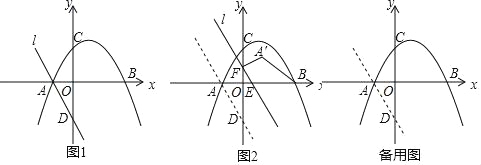
如图1,抛物线y=﹣![]() x2+
x2+![]() x+
x+![]() 与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于C点.经过点A的直线l与y轴交于点D(0,﹣
与x轴分别交于A、B两点(点A在点B的左侧),与y轴交于C点.经过点A的直线l与y轴交于点D(0,﹣![]() ).
).
(1)求A、B两点的坐标及直线l的表达式;
(2)如图2,直线l从图中的位置出发,以每秒1个单位的速度沿x轴的正方向运动,运动中直线l与x轴交于点E,与y轴交于点F,点A 关于直线l的对称点为A′,连接FA′、BA′,设直线l的运动时间为t(t>0)秒.探究下列问题:
①请直接写出A′的坐标(用含字母t的式子表示);
②当点A′落在抛物线上时,求直线l的运动时间t的值,判断此时四边形A′BEF的形状,并说明理由;
(3)在(2)的条件下,探究:在直线l的运动过程中,坐标平面内是否存在点P,使得以P,A′,B,E为顶点的四边形为矩形?若存在,请直接写出点P的坐标; 若不存在,请说明理由.
【答案】(1)y=﹣![]() x﹣
x﹣![]() ;(2)见解析(3)存在
;(2)见解析(3)存在
【解析】
(1)通过解方程﹣![]() x2+
x2+![]() x+
x+![]() =0得A(1,0),B(3,0),然后利用待定系数法确定直线l的解析式;
=0得A(1,0),B(3,0),然后利用待定系数法确定直线l的解析式;
(2)①作A′H⊥x轴于H,如图2,利用OA=1,OD=![]() 得到∠OAD=60°,再利用平移和对称的性质得到EA=EA′=t,∠A′EF=∠AEF=60°,然后根据含30度的直角三角形三边的关系表示出A′H,EH即可得到A′的坐标;
得到∠OAD=60°,再利用平移和对称的性质得到EA=EA′=t,∠A′EF=∠AEF=60°,然后根据含30度的直角三角形三边的关系表示出A′H,EH即可得到A′的坐标;
②把A′(![]() t1,
t1,![]() t)代入y=
t)代入y=![]() x2+
x2+![]() x+
x+![]() 得
得![]() (
(![]() t1)2+
t1)2+![]() (
(![]() t1)+
t1)+![]() =
=![]() t,解方程得到t=2,此时A′点的坐标为(2,
t,解方程得到t=2,此时A′点的坐标为(2,![]() ),E(1,0),然后通过计算得到AF=BE=2,A′F∥BE,从而判断四边形A′BEF为平行四边形,然后加上EF=BE可判定四边形A′BEF为菱形;
),E(1,0),然后通过计算得到AF=BE=2,A′F∥BE,从而判断四边形A′BEF为平行四边形,然后加上EF=BE可判定四边形A′BEF为菱形;
(3)讨论:当A′B⊥BE时,四边形A′BEP为矩形,利用点A′和点B的横坐标相同得到![]() t1=3,解方程求出t得到A′(3,
t1=3,解方程求出t得到A′(3,![]() ),再利用矩形的性质可写出对应的P点坐标;当A′B⊥EA′,如图4,四边形A′BPE为矩形,作A′Q⊥x轴于Q,先确定此时A′点的坐标,然后利用点的平移确定对应P点坐标.
),再利用矩形的性质可写出对应的P点坐标;当A′B⊥EA′,如图4,四边形A′BPE为矩形,作A′Q⊥x轴于Q,先确定此时A′点的坐标,然后利用点的平移确定对应P点坐标.
(1)当y=0时,﹣![]() x2+
x2+![]() =0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),
=0,解得x1=﹣1,x2=3,则A(﹣1,0),B(3,0),
设直线l的解析式为y=kx+b,
把A(﹣1,0),D(0,﹣![]() )代入得
)代入得![]() ,解得
,解得![]() ,
,
∴直线l的解析式为y=﹣![]() x﹣
x﹣![]() ;
;
(2)①作A′H⊥x轴于H,如图,

∵OA=1,OD=![]() ,
,
∴∠OAD=60°,
∵EF∥AD,
∴∠AEF=60°,
∵点A 关于直线l的对称点为A′,
∴EA=EA′=t,∠A′EF=∠AEF=60°,
在Rt△A′EH中,EH=![]() EA′=
EA′=![]() t,A′H=
t,A′H=![]() EH=
EH=![]() t,
t,
∴OH=OE+EH=t﹣1+![]() t=
t=![]() t﹣1,
t﹣1,
∴A′(![]() t﹣1,
t﹣1,![]() t);
t);
②把A′(![]() t﹣1,
t﹣1,![]() t)代入y=﹣
t)代入y=﹣![]() x2+
x2+![]() x+
x+![]() 得﹣
得﹣![]() (
(![]() t﹣1)2+
t﹣1)2+![]() (
(![]() t﹣1)+
t﹣1)+![]() =
=![]() t,
t,
解得t1=0(舍去),t2=2,
∴当点A′落在抛物线上时,直线l的运动时间t的值为2;
此时四边形A′BEF为菱形,理由如下:
当t=2时,A′点的坐标为(2,![]() ),E(1,0),
),E(1,0),
∵∠OEF=60°
∴OF=![]() OE=
OE=![]() ,EF=2OE=2,
,EF=2OE=2,
∴F(0,![]() ),
),
∴A′F∥x轴,
∵A′F=BE=2,A′F∥BE,
∴四边形A′BEF为平行四边形,
而EF=BE=2,
∴四边形A′BEF为菱形;
(3)存在,如图:

当A′B⊥BE时,四边形A′BEP为矩形,则![]() t﹣1=3,解得t=
t﹣1=3,解得t=![]() ,则A′(3,
,则A′(3,![]() ),
),
∵OE=t﹣1=![]() ,
,
∴此时P点坐标为(![]() ,
,![]() );
);
当A′B⊥EA′,如图,四边形A′BPE为矩形,作A′Q⊥x轴于Q,

∵∠AEA′=120°,
∴∠A′EB=60°,
∴∠EBA′=30°
∴BQ=![]() A′Q=
A′Q=![]()
![]() t=
t=![]() t,
t,
∴![]() t﹣1+
t﹣1+![]() t=3,解得t=
t=3,解得t=![]() ,
,
此时A′(1,![]() ),E(
),E(![]() ,0),
,0),
点A′向左平移![]() 个单位,向下平移
个单位,向下平移![]() 个单位得到点E,则点B(3,0)向左平移
个单位得到点E,则点B(3,0)向左平移![]() 个单位,向下平移
个单位,向下平移![]() 个单位得到点P,则P(
个单位得到点P,则P(![]() ,﹣
,﹣![]() ),
),
综上所述,满足条件的P点坐标为(![]() ,
,![]() )或(
)或(![]() ,﹣
,﹣![]() ).
).

【题目】某商场,为了吸引顾客,在“白色情人节”当天举办了商品有奖酬宾活动,凡购物满200元者,有两种奖励方案供选择:一是直接获得20元的礼金券,二是得到一次摇奖的机会.已知在摇奖机内装有2个红球和2个白球,除颜色外其它都相同,摇奖者必须从摇奖机内一次连续摇出两个球,根据球的颜色(如表)决定送礼金券的多少.
球 | 两红 | 一红一白 | 两白 |
礼金券(元) | 18 | 24 | 18 |
(1)请你用列表法(或画树状图法)求一次连续摇出一红一白两球的概率.
(2)如果一名顾客当天在本店购物满200元,若只考虑获得最多的礼品券,请你帮助分析选择哪种方案较为实惠.





