ЬтФПФкШн
ЁОЬтФПЁПЃЈжЊЪЖЩњГЩЃЉЮвУЧвбОжЊЕРЃЌЭЈЙ§МЦЫуМИКЮЭМаЮЕФУцЛ§ПЩвдБэЪОвЛаЉДњЪ§КуЕШЪНЃЎР§ШчЭМ1ПЩвдЕУЕНЃЈa+bЃЉ2ЃНa2+2ab+b2ЃЌЛљгкДЫЃЌЧыНтД№ЯТСаЮЪЬтЃК

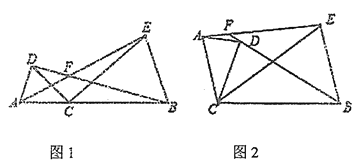
ЃЈ1ЃЉИљОнЭМ2ЃЌаДГівЛИіДњЪ§КуЕШЪНЃКЁЁ ЁЁЃЎ
ЃЈ2ЃЉРћгУЃЈ1ЃЉжаЕУЕНЕФНсТлЃЌНтОіЯТУцЕФЮЪЬтЃКШєa+b+cЃН10ЃЌab+ac+bcЃН35ЃЌдђa2+b2+c2ЃНЁЁ ЁЁЃЎ
ЃЈ3ЃЉаЁУїЭЌбЇгУЭМ3жаxеХБпГЄЮЊaЕФе§ЗНаЮЃЌyеХБпГЄЮЊbЕФе§ЗНаЮЃЌzеХПэЁЂГЄЗжБ№ЮЊaЁЂbЕФГЄЗНаЮжНЦЌЦДГівЛИіУцЛ§ЮЊЃЈ2a+bЃЉЃЈa+2bЃЉГЄЗНаЮЃЌдђx+y+zЃНЁЁ ЁЁЃЎ
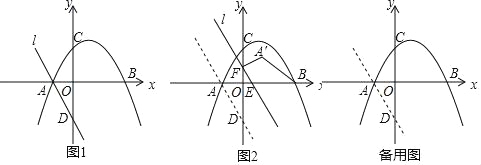
ЃЈжЊЪЖЧЈвЦЃЉЃЈ4ЃЉЪТЪЕЩЯЃЌЭЈЙ§МЦЫуМИКЮЭМаЮЕФЬхЛ§вВПЩвдБэЪОвЛаЉДњЪ§КуЕШЪНЃЌЭМ4БэЪОЕФЪЧвЛИіБпГЄЮЊxЕФе§ЗНЬхЭкШЅвЛИіаЁГЄЗНЬхКѓжиаТЦДГЩвЛИіаТГЄЗНЬхЃЌЧыФуИљОнЭМ4жаЭМаЮЕФБфЛЏЙиЯЕЃЌаДГівЛИіДњЪ§КуЕШЪНЃКЁЁ ЁЁЃЎ
ЁОД№АИЁПЃЈ1ЃЉЃЈa+b+cЃЉ2ЃНa2+b2+c2+2ab+2ac+2bcЃЛЃЈ2ЃЉ30ЃЛЃЈ3ЃЉ9ЃЛЃЈ4ЃЉx3ЉxЃНЃЈx+1ЃЉЃЈxЉ1ЃЉx
ЁОНтЮіЁП
ЃЈ1ЃЉвРОне§ЗНаЮЕФУцЛ§ЃНЃЈa+b+cЃЉ2ЃЛе§ЗНаЮЕФУцЛ§ЃНa2+b2+c2+2ab+2ac+2bcЃЌПЩЕУЕШЪНЃЛ
ЃЈ2ЃЉвРОнa2+b2+c2ЃНЃЈa+b+cЃЉ2Љ2abЉ2acЉ2bcЃЌНјааМЦЫуМДПЩЃЛ
ЃЈ3ЃЉвРОнЫљЦДЭМаЮЕФУцЛ§ЮЊЃКxa2+yb2+zabЃЌЖјЃЈ2a+bЃЉЃЈa+2bЃЉЃН2a2+4ab+ab+2b2ЃН2a2+5b2+2abЃЌМДПЩЕУЕНxЃЌyЃЌzЕФжЕЃЎ
ЃЈ4ЃЉИљОндМИКЮЬхЕФЬхЛ§ЃНаТМИКЮЬхЕФЬхЛ§ЃЌСаЪНПЩЕУНсТлЃЎ
ЃЈ1ЃЉгЩЭМ2ЕУЃКе§ЗНаЮЕФУцЛ§ЃНЃЈa+b+cЃЉ2ЃЛе§ЗНаЮЕФУцЛ§ЃНa2+b2+c2+2ab+2ac+2bcЃЌ
ЁрЃЈa+b+cЃЉ2ЃНa2+b2+c2+2ab+2ac+2bcЃЌ
ЙЪД№АИЮЊЃКЃЈa+b+cЃЉ2ЃНa2+b2+c2+2ab+2ac+2bcЃЛ
ЃЈ2ЃЉЁпЃЈa+b+cЃЉ2ЃНa2+b2+c2+2ab+2ac+2bcЃЌ
Ёпa+b+cЃН10ЃЌab+ac+bcЃН35ЃЌ
Ёр102ЃНa2+b2+c2+2ЁС35ЃЌ
Ёрa2+b2+c2ЃН100Љ70ЃН30ЃЌ
ЙЪД№АИЮЊЃК30ЃЛ
ЃЈ3ЃЉгЩЬтвтЕУЃКЃЈ2a+bЃЉЃЈa+2bЃЉЃНxa2+yb2+zabЃЌ
Ёр2a2+5ab+2b2ЃНxa2+yb2+zabЃЌ
Ёр![]() ЃЌ
ЃЌ
Ёрx+y+zЃН9ЃЌ
ЙЪД№АИЮЊЃК9ЃЛ
ЃЈ4ЃЉЁпдМИКЮЬхЕФЬхЛ§ЃНx3Љ1ЁС1xЃНx3ЉxЃЌ
аТМИКЮЬхЕФЬхЛ§ЃНЃЈx+1ЃЉЃЈxЉ1ЃЉxЃЌ
Ёрx3ЉxЃНЃЈx+1ЃЉЃЈxЉ1ЃЉxЃЎ
ЙЪД№АИЮЊЃКx3ЉxЃНЃЈx+1ЃЉЃЈxЉ1ЃЉxЃЎ

 бєЙтПЮЬУПЮЪБзївЕЯЕСаД№АИ
бєЙтПЮЬУПЮЪБзївЕЯЕСаД№АИ