题目内容
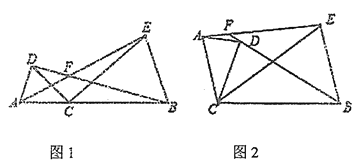
【题目】如图,![]() 是
是![]() 的一个内接三角形,点
的一个内接三角形,点![]() 是劣弧
是劣弧![]() 上一点(点
上一点(点![]() 不与
不与![]() ,
,![]() 重合),设
重合),设![]() ,
,![]() .
.

![]() 当
当![]() 时,求
时,求![]() 的度数;
的度数;
![]() 猜想
猜想![]() 与
与![]() 之间的关系,并给予证明.
之间的关系,并给予证明.
【答案】(1)125°;(2)![]() ;证明见解析;
;证明见解析;
【解析】
(1)在优弧AB上取一点D,连结DA、DB,根据三角形内角和定理得∠AOB=180°﹣∠OAB﹣∠OBA=110°,再根据圆周角定理得∠D=![]() ∠AOB=55°,然后根据圆内接四边形的性质得∠ACB=180°﹣∠D=125°;
∠AOB=55°,然后根据圆内接四边形的性质得∠ACB=180°﹣∠D=125°;
(2)根据三角形内角和定理得∠AOB=180°﹣∠α,根据圆周角定理得∠D=![]() ∠AOB=90°﹣α,然后根据圆内接四边形的性质得∠ACB=180°﹣∠D=180°﹣(90°﹣α)=90°+α.
∠AOB=90°﹣α,然后根据圆内接四边形的性质得∠ACB=180°﹣∠D=180°﹣(90°﹣α)=90°+α.
(1)在优弧AB上取一点D,连结DA、DB,如图,∵∠α=35°,∴∠AOB=180°﹣∠OAB﹣∠OBA=180°﹣2×35°=110°,∴∠D=![]() ∠AOB=55°,∴∠ACB=180°﹣∠D=125°,即β的度数为125°;
∠AOB=55°,∴∠ACB=180°﹣∠D=125°,即β的度数为125°;
(2)∠ACB=90°+α.理由如下:
∵∠AOB=180°﹣2∠α,∴∠D=![]() ∠AOB=
∠AOB=![]() (180°﹣2∠α)=90°﹣α,∴∠ACB=180°﹣∠D=180°﹣(90°﹣α)=90°+α.
(180°﹣2∠α)=90°﹣α,∴∠ACB=180°﹣∠D=180°﹣(90°﹣α)=90°+α.

练习册系列答案
相关题目