题目内容
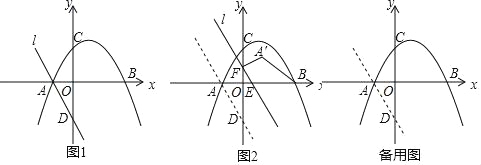
【题目】如图,在平面直角坐标系中,已知点A(﹣5,0),B(5,0),D(2,7),连接AD交y轴于C点.

(1)求C点的坐标;
(2)动点P从B点出发以每秒1个单位的速度沿BA方向运动,同时动点Q从C点出发也以每秒1个单位的速度沿y轴正半轴方向运动(当P点运动到A点时,两点都停止运动).设从出发起运动了x秒.
①请用含x的代数式分别表示P,Q两点的坐标;
②当x=2时,y轴上是否存在一点E,使得△AQE的面积与△APQ的面积相等?若存在,求E的坐标;若不存在,说明理由.
【答案】(1)C(0,5);(2)①P(5﹣x,0),Q(0,5+x);②存在,点E的坐标为:(0,18.2)或(0,﹣4.2),理由见解析
【解析】
(1)作DE⊥x轴,根据点的坐标求出AE、DE、AO,根据等腰直角三角形的性质解答即可;
(2)①根据题意、结合图形解答;
②分E在y轴的正半轴和E在y轴的负半轴两种情况,根据三角形的面积公式计算即可.
(1)作DE⊥x轴,
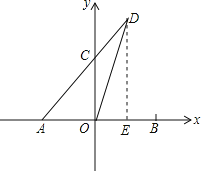
∵A(﹣5,0),D(2,7),
∴AE=DE=7,AO=5,
∵△CAO,△DAE为直角三角形,
∴∠CAO=45°,
∴△CAO是等腰直角三角形,
∴CO=AO=5,
∴C(0,5);
(2)①P(5﹣x,0),Q(0,5+x);
②存在.设E的坐标为(0,y)
当x=2时,△APQ=(5+3)×7÷2=28,
情况一:E在y轴的正半轴
(y﹣7)×5÷2=28
y=18.2
∴E(0,18.2)
情况二:E在y轴的负半轴
(7﹣y)×5÷2=28
y=﹣4.2
∴E(0,﹣4.2)
则点E的坐标为:(0,18.2)或(0,﹣4.2).

 轻松夺冠全能掌控卷系列答案
轻松夺冠全能掌控卷系列答案【题目】为了提高学生书写汉字的能力.增强保护汉字的意识,我区举办了“汉字听写大赛”,经选拔后有50名学生参加决赛,这50名学生同时听写50个汉字,若每正确听写出一个汉字得1分,根据测试成绩绘制出部分频数分布表和部分频数分布直方图如图表:
组别 | 成绩x分 | 频数(人数) |
第1组 | 25≤x<30 | 4 |
第2组 | 30≤x<35 | 6 |
第3组 | 35≤x<40 | 14 |
第4组 | 40≤x<45 | a |
第5组 | 45≤x<50 | 10 |
请结合图表完成下列各题:
(1)求表中a的值;
(2)请把频数分布直方图补充完整;
(3)若测试成绩不低于40分为优秀,则本次测试的优秀率是多少?