题目内容
【题目】魏晋时期的数学家刘徽首创割圆术．为计算圆周率建立了严密的理论和完善的算法．作圆内接正多边形，当正多边形的边数不断增加时，其周长就无限接近圆的周长，进而可用
来求得较为精确的圆周率．祖冲之在刘徽的基础上继续努力，当正多边形的边数增加24576时，得到了精确到小数点后七位的圆周率，这一成就在当时是领先其他国家一千多年，如图，依据“割圆术”，由圆内接正六边形算得的圆周率的近似值是（ ）
A. 0.5 B. 1 C. 3 D. π
【答案】C
【解析】
连接OC、OD，根据正六边形的性质得到∠COD＝60°，得到△COD是等边三角形，得到OC＝CD，根据题意计算即可．
连接OC、OD，
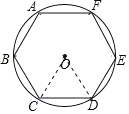
∵六边形ABCDEF是正六边形，
∴∠COD＝60°，又OC＝OD，
∴△COD是等边三角形，
∴OC＝CD，
正六边形的周长：圆的直径＝6CD：2CD＝3，
故选：C．
练习册系列答案
相关题目
