题目内容
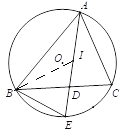
【题目】如图,O是△ABC的外心,I是△ABC的内心,连AI并延长交BC和⊙O于D、E两点.
(1)求证:EB=EI;
(2)若AB=4,AC=3,BE=2,求AI的长.

【答案】(1)见解析;(2)AI=2.
【解析】分析:(1)连接IB,只需证明∠IBE=∠BIE.根据三角形的外角的性质、三角形的内心是三角形的角平分线的交点,以及圆周角定理的推论即可证明.
(2)由(1)可得△BDE∽△ABE,即:DE=![]() ,再由同弦所对的圆周角相等可得:△ADC∽△ABE,即:AB·AC=AD·AE,列出等式求解即可.
,再由同弦所对的圆周角相等可得:△ADC∽△ABE,即:AB·AC=AD·AE,列出等式求解即可.
详解:(1)连BI.如图,
∵I是△ABC的内心,
∴∠BAE=∠CAE,∠ABI=∠CBI,
∵∠CBE=∠CAE,
∴∠BAE=∠CBE,
∴∠BIE=∠ABI+∠BAE,∠IBE=∠CBI+∠CBE,
∴∠IBE=∠BIE,
∴EB=EI.
(2)设AI=x,由(1)可知:∠BAE=∠CBE,且∠E=∠E.
∴△BDE∽△ABE,BE2=ED·EA,即: DE=![]() .
.
又∵∠E=∠C(同弦的圆周角相等),∠BAE=∠CAE.
∴△ADC∽△ABE,AB·AC=AD·AE,
4×3=(x+2)(![]() ),
),
解得x=2,即AI=2.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案
相关题目