题目内容
【题目】如图,点O在直线AB上,OD是∠AOC的平分线,OE是∠BOC的平分线.
(1)图中与∠AOD互余的角是 ,与∠COE互补的角是 ;(把符合条件的角都写出来)
(2)求∠DOE的度数;
(3)如果∠BOF=51°34',∠COE=38°43',请画出射线OF,求∠COF的度数.

【答案】(1)∠COE、∠BOE;∠AOE;(2)90°;(3)作图见解析,∠COF的度数为129°或25°52'.
【解析】
(1)根据![]() 是
是![]() 的平分线,
的平分线,![]() 是
是![]() 的平分线即可写出图中与
的平分线即可写出图中与![]() 互余的角,与
互余的角,与![]() 互补的角;
互补的角;
(2)结合(1)即可求出![]() 的度数;
的度数;
(3)根据![]() ,
,![]() ,即可画出射线
,即可画出射线![]() ,并求得
,并求得![]() 的度数.
的度数.
解:(1)∵OD是∠AOC的平分线,OE是∠BOC的平分线,∴∠AOD=∠COD![]() AOC,
AOC,
,∠BOE=∠COE![]() BOC,∴∠DOC+∠EOC=90°,∴与∠AOD互余的角有:∠COE、∠BOE;
BOC,∴∠DOC+∠EOC=90°,∴与∠AOD互余的角有:∠COE、∠BOE;
与∠COE互补的角有:∠AOE.
故答案为:∠COE、∠BOE;∠AOE;
(2)∵OD是∠AOC的平分线,OE是∠BOC的平分线,
∴∠AOD=∠COD,∠COE=∠BOE,
∵∠AOD+∠COD+∠COE+∠BOE=180°,
∴∠DOE=∠COD+∠COE=90°;
(3)如图,
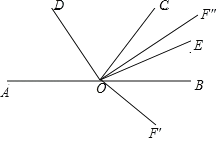
射线OF'和OF″即为所求作的图形,
∠BOF=51°34',∠COE=38°43',
∠COF'=∠BOC+∠BOF=129°,
或∠COF″=∠BOC﹣∠BOF=25°52',
答:∠COF的度数为129°或25°52'.

练习册系列答案
 口算小状元口算速算天天练系列答案
口算小状元口算速算天天练系列答案
相关题目