题目内容
【题目】已知,四边形ABCD是菱形,点M、N分别在AB、AD上,且BM=DN,MG∥AD,NF∥AB,点F、G分别在BC、CD上,MG与NF相交于点E;
(1)如图,求证:四边形AMEN是菱形;
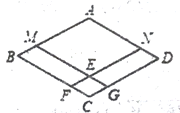
(2)如图,连接AC,在不添加任何辅助线的情况下,请直接写出面积相等的四边形;
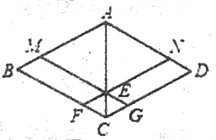
【答案】(1)见解析;(2)S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() .
.
【解析】
(1)由MG∥AD,NF∥AB,可证得四边形AMEN是平行四边形,又由四边形ABCD是菱形,BM=DN,可得AM=AN,即可证得四边形AMEN是菱形;
(2)易得四边形CGEF是菱形;即可得S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,继而求得答案.
,继而求得答案.
(1)证明:∵MG∥AD,NF∥AB,
∴四边形AMEN是平行四边形,
∴四边形ABCD是菱形,
∴AB=AD,
∵BM=DN,
∴ABBM=ADDN,
∴AM=AN,
∴四边形AMEN是菱形;
(2)∵四边形AMEN是菱形,
∴S![]() =S
=S![]() ,
,
同理:四边形CGEF是菱形,
∴S![]() =S
=S![]() ,
,
∵四边形ABCD是菱形,
∴S![]() =S
=S![]() ,
,
∴S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() ,S
,S![]() =S
=S![]() .
.

练习册系列答案
相关题目