题目内容
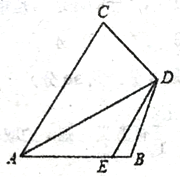
【题目】如图:四边形ABDC中,CD=BD,E为AB上一点,连接DE,且∠CDE=∠B.若∠CAD=∠BAD=30°,AC=5,AB=3,则EB=______________。
【答案】![]()
【解析】
如图,作DM⊥AC于M,DN⊥AB于N.首先证明Rt△DMC≌Rt△DNB,推出CM=BN,△ADM≌△ADN,推出AM=AB,再证明DE∥AC,推出∠ADE=∠CAD=∠DAB=30°,推出AE=DE,推出∠DEN=60°,在Rt△ADN中,可得DN=ANtan30°=![]() ,在Rt△EDN中,可得DE=DN÷cos30°=
,在Rt△EDN中,可得DE=DN÷cos30°=![]() ,由此即可解决问题.
,由此即可解决问题.
如图,作DM⊥AC于M,DN⊥AB于N.
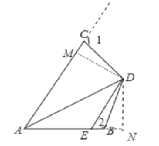
∵∠CAD=∠BAD=30°,DM⊥AC于M,DN⊥AB于N,
∴DN=DM,
在Rt△DMC和Rt△DNB中,
![]() ,
,
∴Rt△DMC≌Rt△DNB,
∴CM=BN,
同理可证△ADM≌△ADN,
∴AM=AB,
∴AC+AB=AM+CM+ANBN=2AM=8,
∴AM=AN=4,
∵∠DCM=∠DBN,
∴∠1=∠2,
∵∠CDE=∠2,
∴∠1=∠CDE,
∴DE∥AC,
∴∠ADE=∠CAD=∠DAB=30°,
∴AE=DE,
∴∠DEN=60°,
在Rt△ADN中,DN=ANtan30°=![]() ,
,
在Rt△EDN中,DE=DN÷cos30°=![]() ,
,
∴AE=![]() ,
,
∴EB=ABAE=3![]() =
=![]() .
.
故答案为![]() .
.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目