ЬтФПФкШн
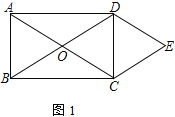
ЁОЬтФПЁПШчЭМЃЌдкБпГЄЮЊ6ЕФе§ЗНаЮABCDФкВПгаСНИіДѓаЁЯрЭЌЕФГЄЗНаЮAEFGЁЂHMCNЃЌHMгыEFЯрНЛгкЕуPЃЌHNгыGFЯрНЛгкЕуQЃЌAG=CM=xЃЌAE=CN=yЃЎ
ЃЈ1ЃЉгУКЌгаxЁЂyЕФДњЪ§ЪНБэЪОГЄЗНаЮAEFGгыГЄЗНаЮHMCNжиЕўВПЗжЕФУцЛ§SЫФБпаЮHPFQЃЌВЂЧѓГіxгІТњзуЕФЬѕМўЃЛ
ЃЈ2ЃЉЕБAG=AEЃЌEF=2PEЪБЃЌ
ЂйAGЕФГЄЮЊ_______ЃЛ
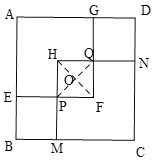
ЂкЫФБпаЮAEFGа§зЊКѓФмгыЫФБпаЮHMCNжиКЯЃЌЧыжИГіИУЭМаЮЫљдкЦНУцФкФмЙЛзїЮЊа§зЊжааФЕФЫљгаЕуЃЌВЂЗжБ№ЫЕУїШчКЮа§зЊЕФЃЎ
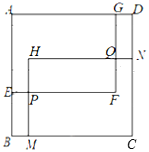
ЁОД№АИЁПЃЈ1ЃЉ![]()
![]() ЃЌ
ЃЌ![]() ЃЛЃЈ2ЃЉЂй4ЃЛЂкМћНтЮіЃЎ
ЃЛЃЈ2ЃЉЂй4ЃЛЂкМћНтЮіЃЎ
ЁОНтЮіЁП
ИљОнОиаЮКЭе§ЗНаЮЕФаджЪПЩxЁЂyБэЪОГіPHЁЂPFЕФГЄЃЌРћгУГЄЗНаЮУцЛ§ЙЋЪНМДПЩЕУ
ЃЈ1ЃЉЁпAG=CM=xЃЌAE=CN=yЃЌЫФБпаЮABCDЪЧе§ЗНаЮЃЌ
Ёр![]()
![]() ЃЌ
ЃЌ![]()
![]() ЃЌ
ЃЌ
Ёр![]()
![]() ЃЌ
ЃЌ![]()
![]()
ЁржиЕўВПЗжГЄЗНаЮЕФУцЛ§ЮЊЃК![]()
![]() ЃЌ
ЃЌ
ЁпГЄЗНаЮAEFGгыГЄЗНаЮHMCNгажиЕўВПЗжЃЌе§ЗНаЮABCDБпГЄЮЊ6ЃЌ
Ёр3<AG<6ЃЌМД![]() ЃЎ
ЃЎ
ЃЈ2ЃЉЂйЁпAG=AE=EFЃЌEF=2PEЃЌ
ЁрPE=![]() AGЃЌ
AGЃЌ
ЁпDG=PEЃЌAD=6ЃЌ
ЁрAD=AG+DG=AG+![]() AG=6ЃЌ
AG=6ЃЌ
НтЕУЃКAG=4ЃЌ
ЙЪД№АИЮЊЃК4
ЂкШчЭМЃЌСЌНгHFЁЂPQЃЌЩшЯрНЛЕФЕуЮЊЕуOЃЌ
ЁпAG=AEЃЌEF=2PEЃЌ
ЁрЫФБпаЮAEFGЁЂ![]() ЖМЪЧе§ЗНаЮЃЌЕу
ЖМЪЧе§ЗНаЮЃЌЕу![]() МШЪЧ
МШЪЧ![]() ЕФжаЕувВЪЧ
ЕФжаЕувВЪЧ![]() ЕФжаЕуЃЌЕу
ЕФжаЕуЃЌЕу![]() МШЪЧ
МШЪЧ![]() ЕФжаЕувВЪЧ
ЕФжаЕувВЪЧ![]() ЕФжаЕуЃЌ
ЕФжаЕуЃЌ
ЁрИУЭМаЮЫљдкЦНУцЩЯПЩвдзїЮЊа§зЊжааФЕФЕуЮЊЕу![]() ЁЂЕу
ЁЂЕу![]() ЁЂЕу
ЁЂЕу![]() ЃЌ
ЃЌ
ЫФБпаЮ![]() ШЦзХЕу
ШЦзХЕу![]() ФцЪБеыЗНЯђЃЈЛђЫГЪБеыЗНЯђЃЉа§зЊ
ФцЪБеыЗНЯђЃЈЛђЫГЪБеыЗНЯђЃЉа§зЊ![]() ЖШПЩгыЫФБпаЮ
ЖШПЩгыЫФБпаЮ![]() жиКЯЃЛ
жиКЯЃЛ
ЫФБпаЮ![]() ШЦзХЕу
ШЦзХЕу![]() ЫГЪБеыЗНЯђа§зЊ
ЫГЪБеыЗНЯђа§зЊ![]() ЖШЃЈЛђФцЪБеыЗНЯђа§зЊ
ЖШЃЈЛђФцЪБеыЗНЯђа§зЊ![]() ЖШЃЉПЩгыЫФБпаЮ
ЖШЃЉПЩгыЫФБпаЮ![]() жиКЯЃЛ
жиКЯЃЛ
ЫФБпаЮ![]() ШЦзХЕу
ШЦзХЕу![]() ФцЪБеыЗНЯђа§зЊ
ФцЪБеыЗНЯђа§зЊ![]() ЖШЃЈЛђЫГЪБеыЗНЯђа§зЊ
ЖШЃЈЛђЫГЪБеыЗНЯђа§зЊ![]() ЖШЃЉПЩгыЫФБпаЮ
ЖШЃЉПЩгыЫФБпаЮ![]() жиКЯЃЎ
жиКЯЃЎ

 КЎМйЬьЕижиЧьГіАцЩчЯЕСаД№АИ
КЎМйЬьЕижиЧьГіАцЩчЯЕСаД№АИ