Question

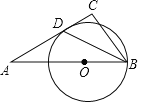
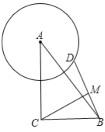
【题目】如图，在Rt△ABC中，∠ACB=90°,AC=4,BC=3,D是以点A为圆心2为半径的圆上一点，连接BD，M为BD的中点，则线段CM长度的最小值为__________．

Answer 1

【答案】

【解析】

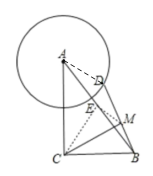
作AB的中点E,连接EM,CE,AD根据三角形中位线的性质和直角三角形斜边中线等于斜边一半求出EM和CE长，再根据三角形的三边关系确定CM长度的范围，从而确定CM的最小值.

解：如图，取AB的中点E，连接CE,ME,AD,

∵E是AB的中点，M是BD的中点，AD=2，

∴EM为△BAD的中位线，

∴ ,

在Rt△ACB中，AC=4,BC=3，

由勾股定理得，AB=

∵CE为Rt△ACB斜边的中线，

∴,

在△CEM中， ,即，

∴CM的最大值为 .

故答案为：.