Question

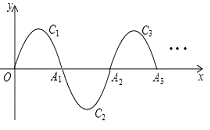
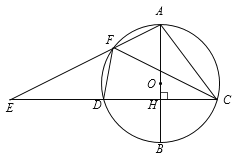
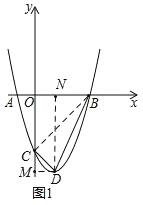
【题目】如图，抛物线y＝x2﹣2x﹣3与x轴分别交于A，B两点（点A在点B的左边），与y轴交于点C，顶点为D．

（1）如图1，求△BCD的面积；

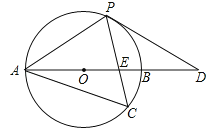
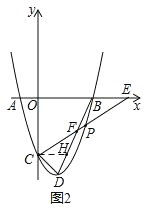
（2）如图2，P是抛物线BD段上一动点，连接CP并延长交x轴于E，连接BD交PC于F，当△CDF的面积与△BEF的面积相等时，求点E和点P的坐标．

Answer 1

【答案】（1）3；（2）E（5，0），P（，﹣）

【解析】

（1）分别求出点C，顶点D，点A，B的坐标，如图1，连接BC，过点D作DM⊥y轴于点M，作点D作DN⊥x轴于点N，证明△BCD是直角三角形，即可由三角形的面积公式求出其面积；

（2）先求出直线BD的解析式，设P（a，a2﹣2a﹣3），用含a的代数式表示出直线PC的解析式，联立两解析式求出含a的代数式的点F的坐标，过点C作x轴的平行线，交BD于点H，则yH＝﹣3，由△CDF与△BEF的面积相等，列出方程，求出a的值，即可写出E，P的坐标．

（1）在y＝x2﹣2x﹣3中，

当x＝0时，y＝﹣3，

∴C（0，﹣3），

当x＝﹣＝1时，y＝﹣4，

∴顶点D（1，﹣4），

当y＝0时，

x1＝﹣1，x2＝3，

∴A（﹣1，0），B（3，0），

如图1，连接BC，过点D作DM⊥y轴于点M，作点D作DN⊥x轴于点N，

∴DC2＝DM2+CM2＝2，BC2＝OC2+OB2＝18，DB2＝DN2+BN2＝20，

∴DC2+BC2＝DB2，

∴△BCD是直角三角形，

∴S△BCD＝DCBC＝×3＝3；

（2）设直线BD的解析式为y＝kx+b，

将B（3，0），D（1，﹣4）代入，

得，

解得，k＝2，b＝﹣6，

∴yBD＝2x﹣6，

设P（a，a2﹣2a﹣3），直线PC的解析式为y＝mx﹣3，

将P（a，a2﹣2a﹣3）代入，

得am＝a2﹣2a﹣3，

∵a≠0，

∴解得，m＝a﹣2，

∴yPC＝（a﹣2）x﹣3，

当y＝0时，x＝，

∴E（，0），

联立，

解得，，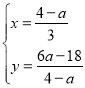

∴F（，），

如图2，过点C作x轴的平行线，交BD于点H，则yH＝﹣3，

∴H（，﹣3），

∴S△CDF＝CH（yF﹣yD），S△BEF＝BE（﹣yF），

∴当△CDF与△BEF的面积相等时，

CH（yF﹣yD）＝BE（﹣yF），

即×（+4）＝（﹣3）（﹣），

解得，a1＝4（舍去），a2＝，

∴E（5，0），P（，﹣）．