Question

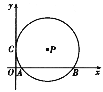
【题目】如图，抛物线y＝ax2+bx﹣3经过点A（2，﹣3），与x轴负半轴交于点B，与y轴交于点C，且OC＝3OB．

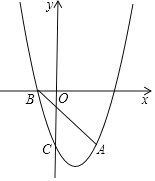
（1）求抛物线的解析式；

（2）抛物线的对称轴上有一点P，使PB+PC的值最小，求点P的坐标；

（3）点M在抛物线上，点N在抛物线的对称轴上，是否存在以点A，B，M，N为顶点的四边形是平行四边形？若存在，直接写出所有符合条件的点M的坐标；若不存在，请说明理由．

Answer 1

【答案】（1） （2）点P的坐标；（3）M

【解析】

（1）待定系数法即可得到结论；

（2）根据线段垂直平分线上的点到线段两端点的距离相等，可得M在对称轴上，根据两点之间线段最短，可得M点在线段AB上，根据自变量与函数值的对应关系，可得答案；

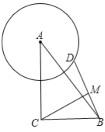
（3）设M（a，a2-2a-3），N（1，n），①以AB为边，则AB∥MN，AB=MN，如图2，过M作ME⊥对称轴于E，AF⊥x轴于F，于是得到△ABF≌△NME，证得NE=AF=3，ME=BF=3，得到M（4，5）或（-2，5）；②以AB为对角线，BN=AM，BN∥AM，如图3，则N在x轴上，M与C重合，于是得到结论．

（1）由得，

把代入，

得，

，

抛物线的解析式为；

（2）连接AB与对称轴直线x=1的交点即为P点的坐标（对称取最值），

设直线AB的解析式为,

将A（2，-3），B（-1，0）代入，得y=-x-1，

将x=1代入，得x=-2，

所以点P的坐标为（1，-2）；

（3）设M（）

①以AB为边，则AB∥MN，如图2，

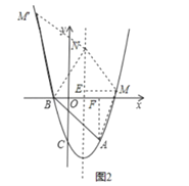
过M作对称轴y于E，AF轴于F，

则

或,

或

∥AM，

如图3，

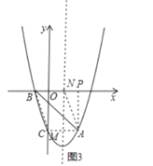
则N在x轴上，M与C重合，

综上所述，存在以点ABMN为顶点的四边形是平行四边形，

或或