题目内容
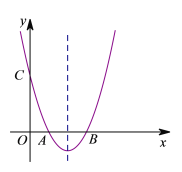
【题目】如图,在平面直角坐标系xOy中,抛物线![]() 与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
与x轴交于A、B两点,与y轴交于点C,对称轴为直线x=2,点A的坐标为(1,0).
(1)求该抛物线的表达式及顶点坐标;
(2)点P为抛物线上一点(不与点A重合),联结PC.当∠PCB=∠ACB时,求点P的坐标;
(3)在(2)的条件下,将抛物线沿平行于![]() 轴的方向向下平移,平移后的抛物线的顶点为点D,点P关于x轴的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.
轴的方向向下平移,平移后的抛物线的顶点为点D,点P关于x轴的对应点为点Q,当OD⊥DQ时,求抛物线平移的距离.

【答案】(1)(2,-1)(2)P(![]() ,
,![]() ).(3)
).(3)![]() .
.
【解析】
(1)用待定系数法即可求得抛物线的表达式,利用顶点公式即可求得抛物线的顶点坐标;
(2)过点P作PN⊥x轴,过点C作CM⊥PN,交NP的延长线于点M,由点B、C的坐标得![]() 为等腰直角三角形,利用等量代换证得∠OCA=∠PCM,利用这对角的正切函数得到MC=3PM,设PM=a,则MC=3a,PN=3-a,得P(3a,3-a)代入抛物线的表达式,即可求得答案;
为等腰直角三角形,利用等量代换证得∠OCA=∠PCM,利用这对角的正切函数得到MC=3PM,设PM=a,则MC=3a,PN=3-a,得P(3a,3-a)代入抛物线的表达式,即可求得答案;
(3)设D的坐标为(2,![]() ),过点D作直线EF∥x轴,交y轴于点E,交PQ的延长线于点F,利用∠OED=∠QFD=∠ODQ=90°,证得∠EOD=∠QDF,再根据其正切函数列出等式即可求得答案.
),过点D作直线EF∥x轴,交y轴于点E,交PQ的延长线于点F,利用∠OED=∠QFD=∠ODQ=90°,证得∠EOD=∠QDF,再根据其正切函数列出等式即可求得答案.
(1)∵A的坐标为(1,0),对称轴为直线x=2,∴点B的坐标为(3,0)
将A(1,0)、B(3,0)代入![]() ,得
,得
![]() 解得:
解得:![]()
所以,![]() .
.
当x=2时,![]()
∴顶点坐标为(2,-1) .
(2)过点P作PN⊥x轴,垂足为点N.过点C作CM⊥PN,交NP的延长线于点M.
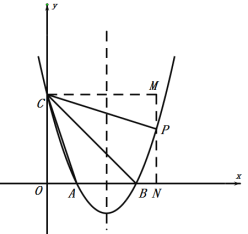
∵∠CON=90°,∴四边形CONM为矩形.
∴∠CMN=90°,CO= MN.
∵![]() ,∴点C的坐标为(0,3)
,∴点C的坐标为(0,3)
∵B(3,0),
∴OB=OC.
∵∠COB=90°,
∴∠OCB=∠BCM = 45°,
又∵∠ACB=∠PCB,
∴∠OCB-∠ACB =∠BCM -∠PCB,即∠OCA=∠PCM.
∴tan∠OCA= tan∠PCM.
∴![]() .
.
设PM=a,则MC=3a,PN=3-a.
∴P(3a,3-a).
将P(3a,3-a)代入![]() ,得
,得
![]() .
.
解得![]() ,
,![]() (舍).∴P(
(舍).∴P(![]() ,
,![]() ).
).
(3)设抛物线平移的距离为m.得![]() ,
,
∴D的坐标为(2,![]() ).
).
过点D作直线EF∥x轴,交y轴于点E,交PQ的延长线于点F.
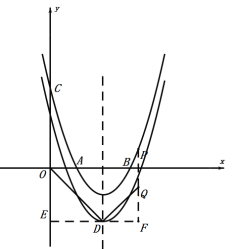
∵∠OED=∠QFD=∠ODQ=90°,
∴∠EOD+∠ODE = 90°,∠ODE+∠QDF = 90°,
∴∠EOD=∠QDF,
∴tan∠EOD = tan∠QDF.
∴![]() .
.
∴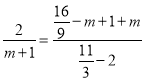 .
.
解得![]() .
.
所以,抛物线平移的距离为![]() .
.