Question

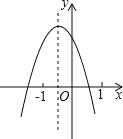
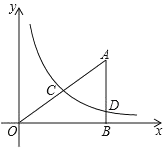
【题目】如图，已知Rt△ABO，点B在轴上，∠ABO=90°，∠AOB=30°，OB=，反比例函数的图象经过OA的中点C，交AB于点D.

（1）求反比例函数的表达式；

（2）求△OCD的面积；

（3）点P是轴上的一个动点，请直接写出使△OCP为直角三角形的点P坐标.

Answer 1

【答案】（1）；（2）面积为；（3）P（2，0）或（4，0）

【解析】

（1）解直角三角形求得AB，作CE⊥OB于E，根据平行线分线段成比例定理和三角形中位线的性质求得C的坐标，然后根据待定系数法即可求得反比例函数的解析式；

（2）补形法，求出各点坐标，S△OCD =S△AOB-S△ACD- S△OBD；

（3）分两种情形：①∠OPC=90°．②∠OCP=90°，分别求解即可．

解：（1）∵∠ABO=90°，∠AOB=30°，OB=，

∴AB= OB=2，

作CE⊥OB于E，
∵∠ABO=90°，
∴CE∥AB，
∴OC=AC，
∴OE=BE=OB=，CE=AB=1，

∴C（，1），

∵反比例函数（x＞0）的图象经过OA的中点C，

∴1=，∴k=，

∴反比例函数的关系式为；

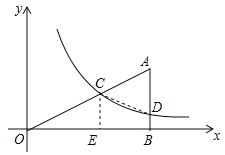
（2）∵OB=，

∴D的横坐标为，

代入得，y=，

∴D（，），

∴BD=，

∵AB=，

∴AD=，

∴S△OCD =S△AOB-S△ACD- S△OBD =OBAB-ADBE-BDOB=

（3）当∠OPC=90°时，点P的横坐标与点C的横坐标相等，C（2，2），
∴P（2，0）．
当∠OCP=90°时．
∵C（2，2），
∴∠COB=45°．
∴△OCP为等腰直角三角形．
∴P（4，0）．
综上所述，点P的坐标为（2，0）或（4，0）．