题目内容
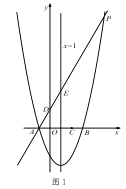
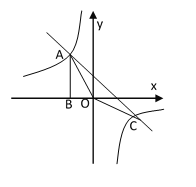
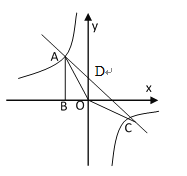
【题目】如图，Rt△ABO的顶点A是双曲线
与直线
在第二象限的交点，AB⊥
轴于B，且
.
（1）求这两个函数的解析式；
（2）求△AOC的面积.
【答案】（1）y=
；（2）4.
【解析】
（1）先根据反比例函数的图象所在的象限判断出k的符号，再由△ABO的面积求出k的值，进而可得出两个函数的解析式；
（2）先把两函数的解析式联立组成方程组，求出x、y的值，得出A、C两点的坐标，再由一次函数的解析式求出直线与y轴的交点D的坐标，然后根据S△AOC=S△AOD+S△COD进行解答即可．
解：(1)设A点坐标为（x,y）,且x<0,y>0
∵
∴xy=-3，∴k=-3
∴y=
(2)在y=-x+2中，当x=0时，y=2，
∴直线y=-x+2与y轴交点D为（0,2）
由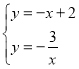
得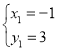
，
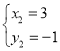
∴A（-1,3），C（3，-1）
∴
=
练习册系列答案
相关题目
【题目】2018年12月4日是第五个国家宪法日，也是第一个“宪法宣传周”．甲、乙两班各选派10名学生参加宪法知识竞赛（满分100分），成绩如下：
成绩 | 85 | 90 | 95 | 100 |
甲班参赛学生/人 | 1 | 1 | 5 | 3 |
乙班参赛学生/人 | 1 | 2 | 3 | 4 |
分别求甲、乙两班参赛学生竞赛成绩的平均数和方差．
