题目内容
【题目】在Rt△ABC中,∠C=90°,Rt△ABC绕点A顺时针旋转到Rt△ADE的位置,点E在斜边AB上,连结BD,过点D作DF⊥AC于点F.
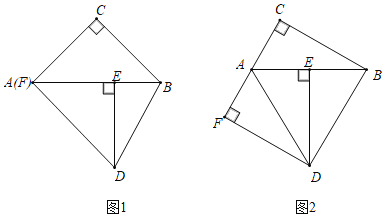
(1)如图1,若点F与点A重合,求证:AC=BC.
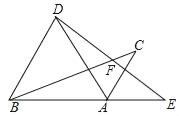
(2)如图2,若点F在线段CA的延长线上,∠DAF=∠DBA,请判断线段AF与BE的数量关系,并说明理由.
【答案】(1)见解析;(2)AF=BE,理由见解析.
【解析】
(1)由旋转的性质可得∠BAC=∠BAD,由垂直的性质可求∠ABC=45°=∠CAB,可得AC=CB;
(2)由“AAS“可证△AFD≌△BED,可得AF=BE.
(1)由旋转得,∠BAC=∠BAD,
∵DF⊥AC,
∴∠CAD=90°,
∴∠BAC=∠BAD=45°,
∵∠ACB=90°,
∴∠ABC=45°=∠CAB,
∴AC=CB;
(2)AF=BE
理由如下:由旋转得,AD=AB,
∴∠ABD=∠ADB,
∵∠DAF=∠ABD,
∴∠DAF=∠ADB,
∴AF∥BD,
∴∠BAC=∠ABD
∵∠ABD=∠FAD,
由旋转得,∠BAC=∠BAD,
∴∠FAD=∠BAC=∠BAD=![]() ×180°=60°,
×180°=60°,
∴△ABD是等边三角形,
∴AD=BD,
在△AFD和△BED中,
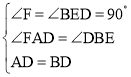
∴△AFD≌△BED(AAS)
∴AF=BE.

练习册系列答案
相关题目