题目内容
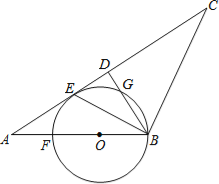
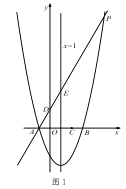
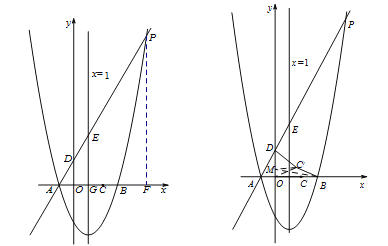
【题目】如图1,对称轴为直线x=1的抛物线y=![]() x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
x2+bx+c,与x轴交于A、B两点(点A在点B的左侧),且点A坐标为(-1,0).又P是抛物线上位于第一象限的点,直线AP与y轴交于点D,与抛物线对称轴交于点E,点C与坐标原点O关于该对称轴成轴对称.
(1)求点 B 的坐标和抛物线的表达式;
(2)当 AE:EP=1:4 时,求点 E 的坐标;
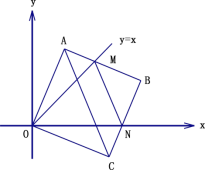
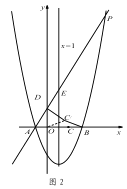
(3)如图 2,在(2)的条件下,将线段 OC 绕点 O 逆时针旋转得到 OC ′,旋转角为 α(0°<α<90°),连接 C ′D、C′B,求 C ′B+ ![]() C′D 的最小值.
C′D 的最小值.
【答案】(1)B(3,0);抛物线的表达式为:y=![]() x2-x-
x2-x-![]() ;(2)E(1,6);(3)C′B+
;(2)E(1,6);(3)C′B+![]() C′D的最小值为
C′D的最小值为![]() .
.
【解析】试题分析:(1)由抛物线的对称轴和过点A ,即可得到抛物线的解析式,令y=0,解方程可得B的坐标;
(2)过点P作PF⊥x轴,垂足为F.由平行线分线段弄成比例定理可得![]() =
=![]() =
=![]() =
=![]() ,从而求出E的坐标;
,从而求出E的坐标;
(3)由E(1,6)、A(-1,0)可得AP的函数表达式为y=3x+3,得到D(0,3).
如图,取点M(0, ![]() ),连接MC′、BM.则可求出OM,BM的长,得到△MOC′∽△C′OD.进而得到MC′=
),连接MC′、BM.则可求出OM,BM的长,得到△MOC′∽△C′OD.进而得到MC′=![]() C′D,由C′B+
C′D,由C′B+![]() C′D=C′B+MC′≥BF可得到结论.
C′D=C′B+MC′≥BF可得到结论.
试题解析:解:(1)∵抛物线y=![]() x2+bx+c的对称轴为直线x=1,∴-
x2+bx+c的对称轴为直线x=1,∴-![]() =1,∴b=-1.
=1,∴b=-1.
∵抛物线过点A(-1,0),∴![]() -b+c=0,解得:c=-
-b+c=0,解得:c=-![]() ,
,
即:抛物线的表达式为:y=![]() x2-x-
x2-x-![]() .
.
令y=0,则![]() x2/span>-x-
x2/span>-x-![]() =0,解得:x1=-1,x2=3,即B(3,0);
=0,解得:x1=-1,x2=3,即B(3,0);
(2)过点P作PF⊥x轴,垂足为F.
∵EG∥PF,AE:EP=1:4,∴![]() =
=![]() =
=![]() =
=![]() .
.
又∵AG=2,∴AF=10,∴F(9,0).
当x=9时,y=30,即P(9,30),PF=30,∴EG=6,∴E(1,6).
(3)由E(1,6)、A(-1,0)可得AP的函数表达式为y=3x+3,则D(0,3).
∵原点O与点C关于该对称轴成轴对称,∴EG=6,∴C(2,0),∴OC′=OC=2.
如图,取点M(0, ![]() ),连接MC′、BM.则OM=
),连接MC′、BM.则OM=![]() ,BM=
,BM=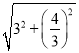 =
=![]() .
.
∵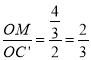 ,
, ![]() ,且∠DOC′=∠C′OD,∴△MOC′∽△C′OD.∴
,且∠DOC′=∠C′OD,∴△MOC′∽△C′OD.∴![]() ,∴MC′=
,∴MC′=![]() C′D,∴C′B+
C′D,∴C′B+![]() C′D=C′B+MC′≥BM=
C′D=C′B+MC′≥BM=![]() ,∴C′B+
,∴C′B+![]() C′D的最小值为
C′D的最小值为![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】观察图形,解答问题:

(1)按下表已填写的形式填写表中的空格:
图① | 图② | 图③ | |
三个角上三个数的积 | 1×(-1)×2=-2 | (-3)×(-4)×(-5)=-60 | |
三个角上三个数的和 | 1+(-1)+2=2 | (-3)+(-4)+(-5)=-12 | |
积与和的商 | (-2)÷2=-1 |
(2)请用你发现的规律求出图④中的数x和图⑤中的数y.