题目内容
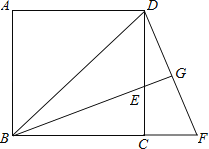
【题目】已知BD是矩形ABCD的对角线,AB=20厘米,BC=40厘米.点P、Q同时从点A出发,分别以2厘米/秒、4厘米/秒的速度由A→B→C→D→A的方向在矩形边上运动,只要Q点回到点A,运动全部停止.设运动时间为t秒.
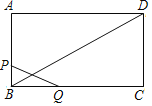
(1)当点P运动在AB(含B点)上,点Q运动在BC(含B、C点)上时,
①设PQ的长为y,求y关于时间t的函数关系式,并写出t的取值范围?
②当t为何值时,△DPQ是等腰三角形?
(2)在P、Q的整个运动过程中,分别判断下列两种情形是否存在?如果存在,请求出t的值;如果不存在,请说明理由.
①PQ与BD平行;
②PQ与BD垂直.
【答案】(1)①y=![]() (5≤t≤10);②当t=
(5≤t≤10);②当t=![]() 时,△DPQ为等腰三角形;(2)①当t=18秒时,PQ与BD平行;②当t=6秒或t=25时,PQ与BD垂直.
时,△DPQ为等腰三角形;(2)①当t=18秒时,PQ与BD平行;②当t=6秒或t=25时,PQ与BD垂直.
【解析】
(1)①根据勾股定理计算斜边PQ的长,可得y关于时间t的函数关系式,因为点P运动在AB(含B点)上,所以0≤t≤10,因为点Q运动在BC(含B、C点)上,所以5≤t≤15,可得5≤t≤10;
②根据图形可知,只有DP=DQ,根据勾股定理列方程得:![]() ,则
,则![]() ,解方程可得结论;
,解方程可得结论;
(2)①根据平行线分线段成比例定理列比例式得:![]() ,则
,则![]() ,解方程可得结论;
,解方程可得结论;
②存在两种情况:
当点P在AB上,点Q在BC上,如图2,此时PA=2t,BP=20﹣2t,BQ=4t﹣20,由PQ⊥BD易证△PBQ∽△DAB,列比例式可得结论;
当点P在BC上,点Q在DA上,如图3,此时BP=2t﹣20,PC=60﹣2t,DQ=4t﹣80,作辅助线,易证△PMQ∽△DAB,列比例式可得结论.
解:(1)由题意可知:PA=2t,BP=20﹣2t,BQ=4t﹣20
①在Rt△PBQ中,![]() =
=![]() =
=![]() (5≤t≤10);
(5≤t≤10);
②由题意可知PQ的长明显小于DP与DQ的长,因此要使△DPQ为等腰三角形,只需满足DP=DQ,
∴![]() ,
,
∴![]() ,
,
∴解得t=![]() (舍),t=
(舍),t=![]() ,
,
∴当t=![]() 时,△DPQ为等腰三角形;
时,△DPQ为等腰三角形;
(2)①由题意知PQ与BD平行,只能点P在BC上,点Q在DC上,如图1,此时BP=2t﹣20,DQ=80﹣4t,
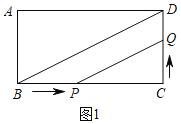
∵PQ∥BD,
∴![]() ,
,
∴![]() ,
,
∴解得t=18,
∴当t=18秒时,PQ与BD平行;
②由题意知PQ与BD垂直,有两种可能,
当点P在AB上,点Q在BC上,如图2,此时PA=2t,BP=20﹣2t,BQ=4t﹣20,
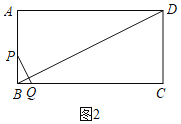
由PQ⊥BD易证△PBQ∽△DAB,
∴![]() ,
,
∴![]() ,
,
解得t=6,
当点P在BC上,点Q在DA上,如图3,此时BP=2t﹣20,PC=60﹣2t,DQ=4t﹣80,
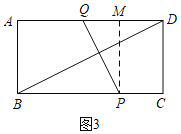
过点P作PM⊥AD,交AD于M点,QM=DQ﹣PC=6t﹣140,
由PQ⊥BD易证△PMQ∽△DAB,
∴![]() ,
,
∴![]() ,
,
解得t=25,
所以当t=6秒或t=25时,PQ与BD垂直.