题目内容
【题目】点A（0，3）和点B（﹣2，1）在直线l1：y＝kx+b上．
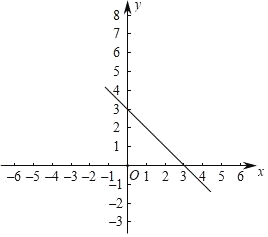
（1）求直线l1的解析式并在平面直角坐标系中画出l1图象；
（2）若直线l1与直线l2：y＝﹣x+3交点C，求C点坐标；
（3）请问在y轴上是否存在点P，使得△ACP是等腰三角形？若存在，请直接写出点P的坐标；若不存在，说明理由．
【答案】（1）y＝x+3；（2）C（0，3）；（3）存在，点P的坐标为（0，﹣3）、（0，3+
）、（0，3﹣）、（0，0）
【解析】
（1）利用待定系数法求出直线l1的解析式,并在平面直角坐标系中找出A、B两点画出直线即可；
（2）将l1与l2的解析式联立，解出二元一次方程组即可求出C点坐标；
（3）设点P（0，m），根据勾股定理可得AC＝3
，AP＝
，CP＝|3﹣m|，此题没有说明哪两边为腰，故需分类讨论①当AC＝AP时，AC＝3，AP＝代入即可求出m；②当AC＝CP时，AC＝3， CP＝|3﹣m|代入即可求出m，③当AP＝CP时，把AP＝，CP＝|3﹣m|代入即可求出m.
解：（1）将点A、B的坐标代入直线l1的函数表达式得：
，解得：
，
故函数表达式为：y＝x+3，
函数图象如下：
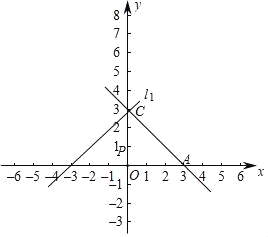
（2）联立l1、l2的表达式并解得：x＝0，y＝3，
故点C（0，3）；
（3）存在，理由：
设点P（0，m），则AC＝3，AP＝，CP＝|3﹣m|，
①当AC＝AP时，则3＝，解得：m＝±3，当m＝3时，P与C重合，故舍去；
②当AC＝CP时，则3＝|3﹣m|，解得：m＝3±3；
③当AP＝CP时，则＝|3﹣m|，m＝0，
故点P的坐标为（0，﹣3）、（0，3+）、（0，3﹣）、（0，0）．
练习册系列答案
相关题目
