题目内容
【题目】如图,已知:在四边形ABFC中,![]() =90
=90![]() 的垂直平分线EF交BC于点D,交AB于点E,且CF=AE
的垂直平分线EF交BC于点D,交AB于点E,且CF=AE

(1)试探究,四边形BECF是什么特殊的四边形;
(2)当![]() 的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
的大小满足什么条件时,四边形BECF是正方形?请回答并证明你的结论.
(特别提醒:表示角最好用数字)
【答案】(1)四边形BECF是菱形,证明见解析(2)当∠A=45。时,菱形BESF是正方形,证明见解析
【解析】(1)四边形BECF是菱形。·························1分
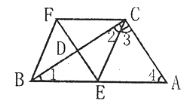
证明:EF垂直平分BC,
∴BF=FC,BE=EC,∴∠1=∠2······2分
∵∠ACB=90°
∴∠1+∠4=90°
∠3+∠2=90°
∴∠3=∠4
∴EC=AE·····················3分
∴BE=AE··················4分
∵CF=AE
∴BE=EC=CF=BF··········5分
∴四边形BECF是菱形·······6分
(2)当∠A=45。时,菱形BESF是正方形··7分
证明:
∵∠A=45。, ∠ACB=90。
∴∠1=45。····························8分
∴∠EBF=2∠A=90。
∴菱形BECF是正方形·················9分
(1)根据中垂线的性质:中垂线上的点到线段两个端点的距离相等,有BE=EC,BF=FC,又因为CF=BE,BE=EC=BF=FC,根据四边相等的四边形是菱形,所以四边形BECF是菱形;
(2)由菱形的性质知,对角线平分一组对角,即当∠ABC=45°时,∠EBF=90°,有菱形为正方形,根据直角三角形中两个角锐角互余得,∠A=45度;

练习册系列答案
 优学名师名题系列答案
优学名师名题系列答案
相关题目




