Question

【题目】已知，在四边形ABCD中，∠F为四边形ABCD的∠ABC的平分线及外角∠DCE的平分线所在的直线构成的锐角，若∠A＝α，∠D＝β，

（1）如图①，当α+β＞180°时，∠F＝____（用含α，β的式子表示）；

（2）如图②，当α+β＜180°时，请在图②中，画出∠F，且∠F＝___（用含α，β的式子表示）；

（3）当α，β满足条件___时，不存在∠F．

Answer 1

【答案】（α+β）﹣90°； 90°﹣（α+β）； α+β＝180°．

【解析】

（1）根据四边形的内角和定理表示出∠BCD，再表示出∠DCE，然后根据角平分线的定义可得∠FBC=∠ABC，∠FCE=∠DCE，三角形的一个外角等于与它不相邻的两个内角的和可得∠F+∠FBC=∠FCE，然后整理即可得解；

（2）与（1）的思路相同，得到∠FBC=∠ABC，∠FCE=∠DCE，由外角性质，得到∠F+∠FBC=∠FCE，通过等量代换，求解即可；

（3）根据∠F的表示，∠F为0时，不存在．

解：（1）如图：

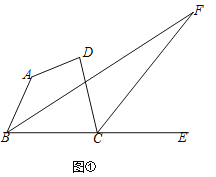
由四边形内角和定理得，∠BCD＝360°﹣∠A﹣∠D﹣∠ABC，

∴∠DCE＝180°﹣（360°﹣∠A﹣∠D﹣∠ABC）＝∠A+∠D+∠ABC﹣180°，

由三角形的外角性质得，∠FCE＝∠F+∠FBC，

∵BF、CF分别是∠ABC和∠DCE的平分线，

∴∠FBC＝∠ABC，∠FCE＝∠DCE，

∴∠F+∠FBC＝（∠A+∠D+∠ABC﹣180°）＝（∠A+∠D）+∠ABC﹣90°，

∴∠F＝（∠A+∠D）﹣90°，

∵∠A＝α，∠D＝β，

∴∠F＝（α+β）﹣90°；

（2）如图3，

由（1）可知，∠BCD＝360°﹣∠A﹣∠D﹣∠ABC，

∴∠DCE＝180°﹣（360°﹣∠A﹣∠D﹣∠ABC）＝∠A+∠D+∠ABC﹣180°，

∴∠FCE＝∠F+∠FBC，

∵∠FBC＝（360°﹣∠ABC），∠FCE＝180°﹣∠DCE，

∴∠F=∠FCE﹣∠FBC=180°﹣（∠A+∠D+∠ABC﹣180°）﹣（360°﹣∠ABC），

∴∠F=90°﹣（∠A+∠D）

∴∠F＝90°﹣（α+β）；

（3）当α+β＝180°时，

∴∠F＝90°﹣，

此时∠F不存在．