题目内容
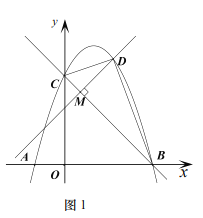
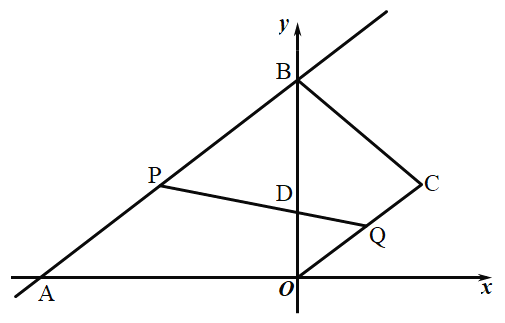
【题目】如图,在直角坐标系中,直线![]() 与x轴,y轴分别交于点A,B,点
与x轴,y轴分别交于点A,B,点![]() 在第一象限内,连结
在第一象限内,连结![]() ,
,![]() ,
,![]() .动点P在
.动点P在![]() 上从点A向终点B匀速运动,同时,动点Q在
上从点A向终点B匀速运动,同时,动点Q在![]() 上从点C向终点O匀速运动,它们同时到达终点,连结
上从点C向终点O匀速运动,它们同时到达终点,连结![]() 交
交![]() 于点D.
于点D.
(1)求点B的坐标和a的值;
(2)当点Q运动到![]() 中点时,连结
中点时,连结![]() ,求
,求![]() 的面积;
的面积;
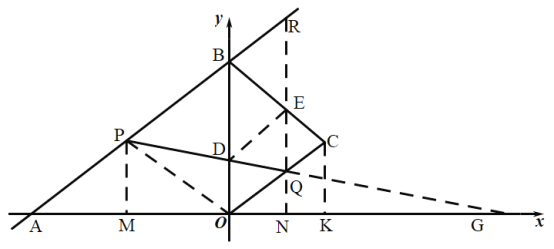
(3)作![]() 交直线
交直线![]() 于点R.
于点R.
①当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长度;
的长度;
②记![]() 交
交![]() 于点E,连结
于点E,连结![]() ,则
,则![]() 的最小值为__________.(直接写出答案)
的最小值为__________.(直接写出答案)
【答案】(1)![]() ,
,![]() ;(2)6;(3)①
;(2)6;(3)①![]() 或
或![]() 或
或![]() ;②
;②![]()
【解析】
(1)根据![]() 令
令![]() 求算B的坐标;再根据
求算B的坐标;再根据![]() ,得出OC的斜率和AB的斜率相等进行求算;
,得出OC的斜率和AB的斜率相等进行求算;
(2)延长PQ与x轴交于G点,根据题意知:P点运动速度是Q点的两倍,得出点Q运动到![]() 中点时,P运动到AB中点,求出PQ的直线解析式从而得出G点的坐标,再根据
中点时,P运动到AB中点,求出PQ的直线解析式从而得出G点的坐标,再根据![]() 求算即可;
求算即可;
(3)①![]() ,设AP=2t,CQ=t,易得:
,设AP=2t,CQ=t,易得:![]()
![]() ,表示出P、Q、R的坐标,再根据
,表示出P、Q、R的坐标,再根据![]() 为等腰三角形分类讨论即可;
为等腰三角形分类讨论即可;
②根据①中P、Q的点坐标表示出PQ的函数解析式,从而求算D点坐标,再表示出E点坐标,根据距离公式表示出DE的长度,配方成顶点式求算最小值.
(1)∵直线![]() 与x轴,y轴分别交于点A,B
与x轴,y轴分别交于点A,B
∴![]()
又∵![]() ,点
,点![]()
∴![]() 即
即![]()
∴![]()
综上所述:B点坐标为![]() ,
,![]() ;
;
(2)延长PQ与x轴交于G点:
由(1)知:AB=10,OC=5, 根据题意知:P点运动速度是Q点的两倍
∴点Q运动到![]() 中点时,P运动到AB中点
中点时,P运动到AB中点
∴![]()
设PQ的解析式为:![]() ,代入得:
,代入得:
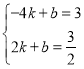 解得:
解得: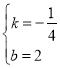
∴PQ的解析式为:![]()
∴![]()
∴![]()
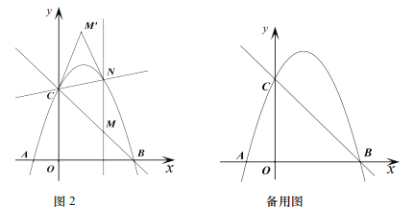
(3)①作![]()
根据题意知:P点运动速度是Q点的两倍,设AP=2t,CQ=t
易得:![]()
∴![]() ,代入得:
,代入得:
![]()
∴![]()
当![]() 时:根据三线合一知:
时:根据三线合一知:
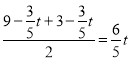 解得:
解得:![]()
∴CQ为![]() ;
;
当![]() 时:通过距离公式得:
时:通过距离公式得:
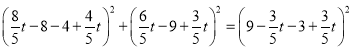 ,解得:
,解得:![]() (舍)
(舍)
∴CQ为![]() ;
;
当![]() 时,通过距离公式得:
时,通过距离公式得:
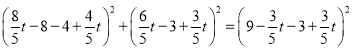 ,解得:
,解得:![]() (舍)
(舍)
∴CQ为![]()
综上所述:当![]() 为等腰三角形时,求
为等腰三角形时,求![]() 的长
的长![]() 或
或![]() 或
或![]() ;
;
②设PQ的解析式为:![]() 代入P、Q:
代入P、Q:
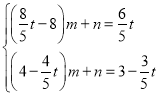 解得:
解得: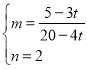
∴![]()
设BC的解析式为:![]() ,代入B、C得:
,代入B、C得:
![]() 解得
解得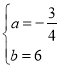
∴BC的解析式为:![]()
∴![]()
∴由距离公式得: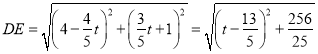
∴当![]() 时,DE有最小值为
时,DE有最小值为![]()
综上所述:DE最小值为![]()

 阅读快车系列答案
阅读快车系列答案