题目内容
【题目】只有1和它本身两个因数且大于1的正整数叫做素数.我国数学家陈景润哥德巴赫猜想的研究中取得了世界领先的成果.哥德巴赫猜想是“每个大于2的偶数都表示为两个素数的和”,如10=3+7.
(1)从7,11,13,17这4个素数中随机抽取一个,则抽到的数是11的概率是_____;
(2)从7,11,13,17这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,用画树状图或列表的方法,求抽到的两个素数之和等于24的概率.
【答案】(1)![]() ;(2)
;(2)![]() .
.
【解析】
(1))四个数中,抽到11只有一种可能,根据概率公式直接计算即可得;
(2)画树状图得到所有等可能的情况,然后再从中找出符合条件的结果数,利用概率公式进行计算即可.
解:(1)在7,11,13,17中,抽到11的概率是![]() ;
;
(2)列表如下:
7 | 11 | 13 | 17 | |
7 | * | 18 | 20 | 24 |
11 | 18 | * | 24 | 28 |
13 | 20 | 24 | * | 30 |
17 | 24 | 28 | 30 | * |
由表可以看出,分别从这4个素数中随机抽取1个数,再从余下的3个数中随机抽取1个数,可能出现的结果有12种,并且他们出现的可能性相等,抽到的两个素数之和等于24的有4种情况.
所以,抽到的两个素数之和等于24的概率为P=![]() .
.

练习册系列答案
相关题目
【题目】“推进全科阅读,培育时代新人”.某学校为了更好地开展学生读书活动,随机调查了九年级50名学生最近一周的读书时间,统计数据如下表:
时间(小时) | 6 | 7 | 8 | 9 | 10 |
人数 | 5 | 8 | 12 | 15 | 10 |
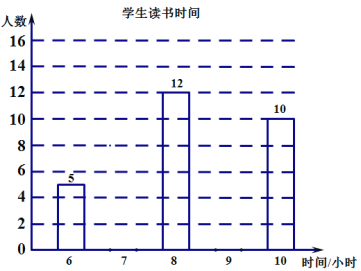
(1)根据上述表格补全下面的条形统计图;
(2)写出这50名学生读书时间的众数、中位数、平均数;
(3)若该校有1000名学生,求最近一周的读书时间不少于7小时的人数?