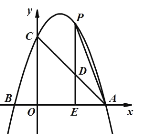题目内容
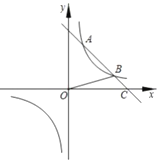
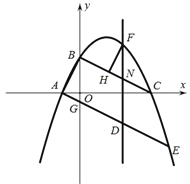
【题目】如图所示,在平面直角坐标系中,抛物线![]() 与y轴交于点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点
与y轴交于点B,与x轴交于点A,C(点A在点C的左侧),A(-1,0),C(4,0),连接AB,BC,点![]() 为y轴负半轴上的一点,连接AG并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线交抛物线于点F,与线段BC交于点N.
为y轴负半轴上的一点,连接AG并延长交抛物线于点E,点D为线段AE上的一个动点,过点D作y轴的平行线交抛物线于点F,与线段BC交于点N.
(1)求抛物线的表达式及直线BC的表达式;
(2)在点D运动的过程中,当FN的值最大时,在线段BC上是否存在一点H,使得FNH与ABC相似,如果存在,求出此时H点的坐标;
(3)当DF=4时,连接DC,四边形ABCD先向上平移一定单位长度后,使点D落在x轴上,然后沿x轴向左平移n(1n4)个单位长度,用含n的表达式表示平移后的四边形与原四边形重叠部分的面积S(直接写出结果).

【答案】(1)直线![]() 的解析式为
的解析式为![]() ,抛物线的解析式为
,抛物线的解析式为![]() ;(2)存在,点
;(2)存在,点![]() 的坐标为
的坐标为![]() ;(3)
;(3)![]()
![]() .
.
【解析】
(1)将点A(-1,0),C(4,0)代入![]() 得出方程组,再解方程组求出a,b即可;根据B、C两点坐标利用待定系数法求出直线BC的解析式即可;
得出方程组,再解方程组求出a,b即可;根据B、C两点坐标利用待定系数法求出直线BC的解析式即可;
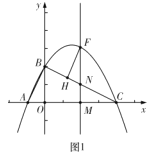
(2)如图2中,设![]() ,则
,则![]() ,构建二次函数求出FN最大时,点F的坐标,证明
,构建二次函数求出FN最大时,点F的坐标,证明![]() 是直角三角形,观察图象可知,只有
是直角三角形,观察图象可知,只有![]() 时,
时,![]() ,求出直线FH的解析式,利用方程组即可求出点H的坐标;
,求出直线FH的解析式,利用方程组即可求出点H的坐标;
(3)根据![]() ,列出方程,求出m的值,分两种情形分别求解即可.
,列出方程,求出m的值,分两种情形分别求解即可.
解:(1)把![]() ,
,![]() 代入
代入![]()
得到![]() ,
,
解得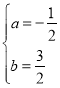 ,
,
∴抛物线的解析式为![]() ,
,
∵![]() ,
,![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
则有![]() ,
,
解得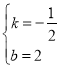 ,
,
∴直线![]() 的解析式为
的解析式为![]() .
.
(2)如图1中,设![]() ,则
,则![]() ,
,
∴![]()
![]() ,
,
∵![]() ,
,
∴![]() 时,
时,![]() 的值最大,此时
的值最大,此时![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() ,
,
∵![]() ,
,![]() ,
,![]() ,
,
∴![]() ,
,
∵![]() 与
与![]() 相似,
相似,
观察图象可知,只有![]() 时,
时, ![]() ,
,
设直线![]() 的解析式为
的解析式为![]() ,
,
把![]() 代入得
代入得![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,
由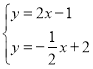 ,解得
,解得![]() ,
,
∴点![]() 的坐标为
的坐标为![]() .
.
(3)∵![]() ,
,![]() ,
,
∴直线![]() 的解析式为
的解析式为![]() ,
,![]() ,
,
∵![]() ,
,
∴![]() ,
,
解得![]() 或3.
或3.
①当![]() 时,如图2中,
时,如图2中,![]() 时,重叠部分是四边形
时,重叠部分是四边形![]() ,
,
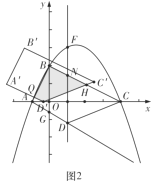
![]() ;
;
如图3中,![]() 时,重叠部分是
时,重叠部分是![]() ,
,
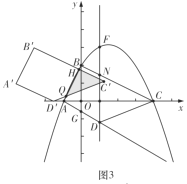
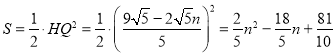 .
.
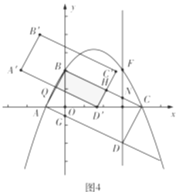
②当![]() 时,如图4中,
时,如图4中,![]() 时,重叠部分是矩形
时,重叠部分是矩形![]() .
.
![]()
![]() .
.

【题目】垫球是排球队常规训练的重要项目之一.下列图表中的数据是甲、乙、丙三人每人十次垫球测试的成绩.测试规则为每次连续接球10个,每垫球到位1个记1分.
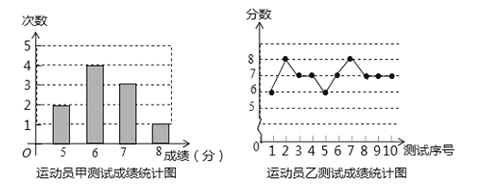
运动员丙测试成绩统计表
测试序号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
成绩(分) | 7 | 6 | 8 |
| 7 | 5 | 8 |
| 8 | 7 |
运动员丙测试成绩的平均数和众数都是7,
(1)成绩表中的![]() __________,
__________,![]() _________;
_________;
(2)若在他们三人中选择一位垫球成绩优秀且较为稳定的接球能手作为自由人,你认为选谁更合适?请用你所学过的统计量加以分析说明(参考数据:三人成绩的方差分别为![]() 、
、![]() 、
、![]() )
)
(3)甲、乙、丙三人相互之间进行垫球练习,每个人的球都等可能的传给其他两人,球从乙手中传出,球传一次甲得到球的概率是____.