题目内容
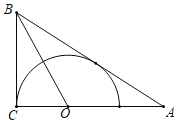
【题目】已知⊙O的半径为3，A为圆内一定点，AO＝1，P为圆上一动点，以AP为边作等腰△APQ，AP＝PQ，∠APQ＝120°，则OQ的最大值为（ ）
A.1+3
B.1+2C.3+D.3
【答案】A
【解析】
以点P为顶点作等腰三角形OPM，OP=PM，可以证明△AOP≌△QMP，可得MQ=OA=1，作
于
，根据三角函数可得OM=
，根据三角形三边关系可得OQ≤OM+MQ= +1，当且仅当M在OQ上时，取等号，即可得结论．
解：如图，
以点P为顶点作等腰三角形OPM，OP＝PM，
∠OPM＝120，
∵∠APQ＝120°，
∴∠OPM＝∠APQ，
∵∠OPA+∠APM＝∠MPQ+∠APM，
∴∠OPA＝∠MPQ，
∵AP＝PQ，OM＝PM，
∴△AOP≌△QMP（SAS），
∴MQ＝OA＝1，
如图，在
中，作于，
∠POM＝30°，
∴OH＝OPcos30°＝
∴OQ≤OM+MQ＝
当且仅当M在OQ上时，取等号，
则OQ的最大值为
故选：A．
练习册系列答案
相关题目
