题目内容
【题目】已知二次函数![]() 的图象与
的图象与![]() 轴交于
轴交于![]() 两点,与
两点,与![]() 轴交于
轴交于![]() 点,点
点,点![]() 在直线
在直线![]() 上,横坐标为
上,横坐标为![]() .
.
(1)确定二次函数![]() 的解析式;
的解析式;
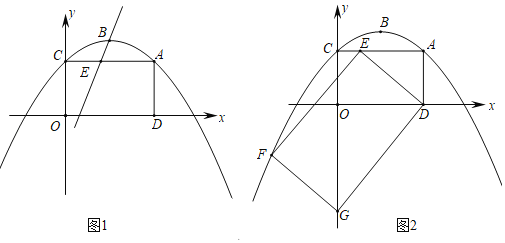
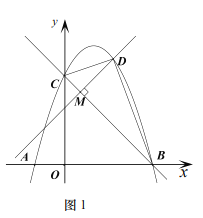
(2)如图1,![]() 时,
时,![]() 交二次函数
交二次函数![]() 的图象于点
的图象于点![]() 的面积记作
的面积记作![]() 为何值时
为何值时![]() 的值最大,并求出
的值最大,并求出![]() 的最大值;
的最大值;
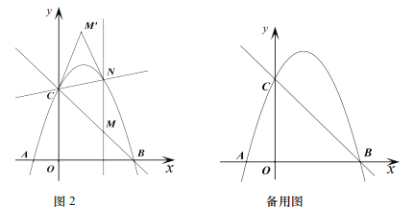
(3)如图2,过点![]() 作
作![]() 轴的平行线交二次函数
轴的平行线交二次函数![]() 的图象于点
的图象于点![]() 点
点![]() 与点
与点![]() 关于直线
关于直线![]() 对称是否存在点
对称是否存在点![]() 使四边形
使四边形![]() 为菱形,若存在直接写出
为菱形,若存在直接写出![]() 的值;若不存在请说明理由.
的值;若不存在请说明理由.
【答案】(1)![]() ;(2)m=
;(2)m=![]() ;
;![]() ;(3)存在,m的值为
;(3)存在,m的值为![]() 或
或![]() .
.
【解析】
(1)把点A、B的坐标代入![]() ,即可得到答案;
,即可得到答案;
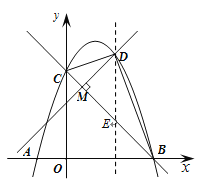
(2)过点D作DE∥![]() 轴,交直线BC于点E,令点D(
轴,交直线BC于点E,令点D(![]() ,
,![]() ),则点E(
),则点E(![]() ,
,![]() ),易证
),易证![]() MED是等腰直角三角形,由
MED是等腰直角三角形,由![]() ,得到二次函数解析式,进而即可求解;
,得到二次函数解析式,进而即可求解;
(3)由题意得:当MN=MC时,四边形![]() 为菱形,设M(m,-m+3),则N(m,
为菱形,设M(m,-m+3),则N(m,![]() ),从而得MN,MC的表达式,列出关于m的方程,进而即可求解.
),从而得MN,MC的表达式,列出关于m的方程,进而即可求解.
(1)A(-1,0)、B(3,0)代入![]() 可得
可得![]() ,解得
,解得![]() ·
·
∴![]()
(2)过点D作DE∥![]() 轴,交直线BC于点E
轴,交直线BC于点E
∵![]()
∴点C(0,3)
∴直线BC:![]() ·
·
令点D(![]() ,
,![]() ),则点E(
),则点E(![]() ,
,![]() )
)
∴DE=![]()
∵OB=OC=3,
∴∠OBC=45°,
∵DE⊥x轴,
∴![]() MED是等腰直角三角形,
MED是等腰直角三角形,
∴MD=![]()
∴![]() ·
·
则![]() 时,
时,![]()
此时,点D(![]() ,
,![]() ),点E(
),点E(![]() ,
,![]() )
)
∴DE=![]() -
-![]() =
=![]() ,
,
∴m=![]() ;
;
(3)由题意得:当MN=MC时,四边形![]() 为菱形,
为菱形,
设M(m,-m+3),则N(m,![]() ),
),
∴MN=![]() ,MC=
,MC=![]() ,
,
∴![]() =
=![]() ,解得:m=
,解得:m=![]() 或
或![]()
![]() 或
或![]() .
.

练习册系列答案
相关题目