题目内容
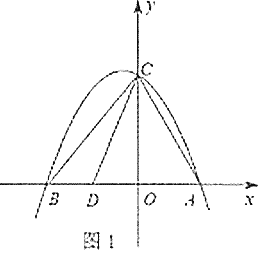
【题目】在平面直角坐标系xOy中(如图),已知抛物线![]() 经过点
经过点![]() 和
和![]() ,其顶点为C.
,其顶点为C.

(1)求抛物线的解析式和顶点C的坐标;
(2)我们把坐标为(n,m)的点叫做坐标为(m,n)的点的反射点,已知点M在这条抛物线上,它的反射点在抛物线的对称轴上,求点M的坐标;
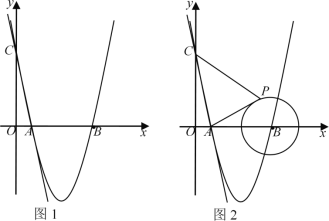
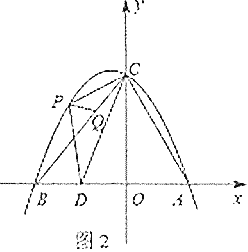
(3)点P是抛物线在第一象限部分上的一点,如果∠POA=∠ACB,求点P的坐标.
【答案】(1)![]() ,顶点C的坐标为:(1,4);(2)点M的坐标为(
,顶点C的坐标为:(1,4);(2)点M的坐标为(![]() ,1)或(
,1)或(![]() ,1);(3)点P的坐标为(
,1);(3)点P的坐标为(![]() ,
,![]() ).
).
【解析】
(1)将点![]() 和
和![]() 代入
代入![]() 即可求出;
即可求出;
(2)设点M的坐标为(n,m),则其反射点的坐标为(m,n),根据点M的反射点在抛物线的对称轴上得到m=1,即M(n,1),将点M坐标代入解析式求出n即可得到坐标;
(3)根据点![]() 和
和![]() 求出AB=
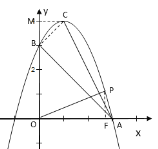
求出AB=![]() ,过点C作CM⊥y轴与M,根据C(1,4),求出CM=BM=1,推出∠ABC=90°,
,过点C作CM⊥y轴与M,根据C(1,4),求出CM=BM=1,推出∠ABC=90°,![]() ,设点P的坐标为(x,
,设点P的坐标为(x,![]() ),过点P作PF⊥x轴于F,则∠OFP=∠ABC=90°,证明△POF∽△CAB,列关系式求出x即可得到点P的坐标.
),过点P作PF⊥x轴于F,则∠OFP=∠ABC=90°,证明△POF∽△CAB,列关系式求出x即可得到点P的坐标.
(1)将点![]() 和
和![]() 代入
代入![]() 得
得
![]() ,解得
,解得![]() ,
,
∴![]() =
=![]() ,
,
∴顶点C的坐标为:(1,4);
(2)设点M的坐标为(n,m),则其反射点的坐标为(m,n),
∵点M的反射点在抛物线的对称轴上,
∴m=1,即M(n,1),
代入![]() 中,得
中,得![]() ,
,
∴![]() ,
,
∴点M的坐标为(![]() ,1)或(
,1)或(![]() ,1);
,1);
(3)∵点![]() 和
和![]() ,
,
∴OA=OB=3,
∴AB=![]() ,
,
∴∠ABO=∠BAO=45°,
过点C作CM⊥y轴与M,
∵C(1,4),
∴CM=BM=1,
∴∠CBM=∠BCM=45°,
∴∠ABC=90°,
∴![]() ,
,
设点P的坐标为(x,![]() ),
),
过点P作PF⊥x轴于F,则∠OFP=∠ABC=90°,
∵∠POA=∠ACB,
∴△POF∽△CAB,
∴![]() ,
,
∴![]() ,
,
解得x=![]() 或x=
或x=![]() (不合题意,舍去),
(不合题意,舍去),
∴![]() =
=![]() ,
,
∴点P的坐标为(![]() ,
,![]() ).
).

 春雨教育同步作文系列答案
春雨教育同步作文系列答案