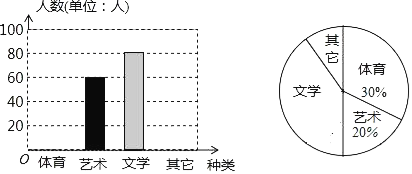
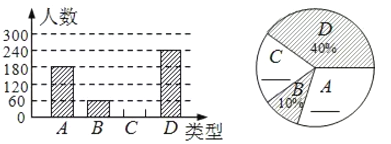
��Ŀ����
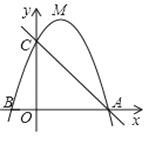
����Ŀ����ͼ1����ƽ��ֱ������ϵ�У�ֱ��![]() ��
��![]() �ᡢ
�ᡢ![]() ��ֱ���
��ֱ���![]() ��
��![]() ���㣬������
���㣬������![]() ����
����![]() ��
��![]() ���㣬��
���㣬��![]() �����һ������Ϊ
�����һ������Ϊ![]() ��
��
��1���������ߵĽ���ʽ��![]() �����ꣻ
�����ꣻ
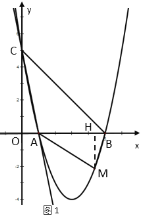
��2������MΪx���·���������һ���㣬����MA��MB��BC������M�˶���ijһλ��ʱ���ı���AMBC���������ʱ��M�����꼰�ı���AMBC�������
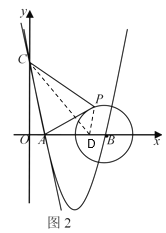
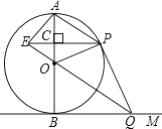
��3����ͼ2����![]() ���ǰ뾶Ϊ2�ġ�
���ǰ뾶Ϊ2�ġ�![]() ��һ���㣬����
��һ���㣬����![]() ��
��![]() ������
������![]() �˶���ijһλ��ʱ��
�˶���ijһλ��ʱ��![]() ��ֵ��СΪ_________��(ֱ��д�����)
��ֵ��СΪ_________��(ֱ��д�����)
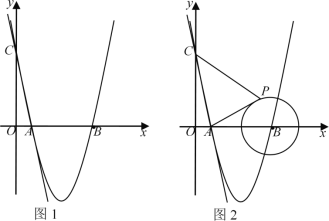
���𰸡���1��![]() ��B(5��0)����2��M(3,-4)ʱ���ı���AMBC����������������18����3��
��B(5��0)����2��M(3,-4)ʱ���ı���AMBC����������������18����3��![]()
��������
(1)��ֱ��y=-5x+5���A��C���꣬�ô���ϵ�����������߽���ʽ��������õ�B���ꣻ
(2)��x����ı���AMBC�ֳɡ�ABC���ABM���ɵ�A��B��C������ABC��������M������Ϊm������M��x��Ĵ��߶�MH��������m��ʾMH�ij����������ABM��������õ���ABM�����m�Ķ��κ�����ϵʽ���Ҷ�Ӧ��aֵС��0���䷽�����mΪ��ֵʱȡ�����ֵ���������M������ı���AMBC��������ֵ��
(3)����D����Ϊ(4,0)���ɵ�BD=1��������![]() ���ټ��Ϲ����ǡ�PBD=��ABP���������߶�Ӧ�ɱ����Ҽн���ȿ�֤��PBD�ס�ABP����
���ټ��Ϲ����ǡ�PBD=��ABP���������߶�Ӧ�ɱ����Ҽн���ȿ�֤��PBD�ס�ABP����![]() �������Ʊ�
�������Ʊ�![]() �������õ�PD=
�������õ�PD=![]() AP�����Ե�C��P��D��ͬһֱ����ʱ��PC+
AP�����Ե�C��P��D��ͬһֱ����ʱ��PC+![]() PA=PC+PD=CD��С���������ľ��빫ʽ�������CD�ij�.
PA=PC+PD=CD��С���������ľ��빫ʽ�������CD�ij�.
(1)ֱ��y=-5x+5��x=0ʱ��y=5��
��C(0,5)��
��y=-5x+5=0ʱ�����x=1��
��A(1,0)��
��������![]() ����A��C���㣬
����A��C���㣬
��![]() �����
�����![]() ��
��
�������߽���ʽΪ![]() ��
��
��![]() =0ʱ�����
=0ʱ�����![]() ��
��![]() ��
��
��B��5,0����
��2����ͼ1������M��MH��x����H��
�� A(1,0)��B(5,0),C(0,5)��
��AB=5-1=4��OC=5��
��![]() ��
��
�ߵ�MΪx���·��������ϵĵ�
����M(m,m2-6m+5)(1<m<5)��
��MH=|m2-6m+5|=-m2+6m-5��
��![]() ��
��
��S�ı���AMBC=S��ABC+S��ABM=![]() ��
��
�൱m=3����M(3,-4)ʱ���ı���AMBC����������������18��
��3����ͼ2����x����ȡ��D��4,0��������PD��CD��
��BD=5-4=1��
��AB=4��BP=2��
��![]() ��
��
�ߡ�PBD=��ABP��
���PBD�ס�ABP��
��![]() ��
��
��PD=![]() AP��
AP��
��PC+![]() PA=PC+PD��
PA=PC+PD��
����C.P��D��ͬһֱ����ʱ��PC+![]() PA=PC+PD=CD��С��
PA=PC+PD=CD����
��![]() ��
��
��PC+![]() PA����СֵΪ
PA����СֵΪ![]() ��
��
�ʴ�Ϊ��![]() .
.