题目内容
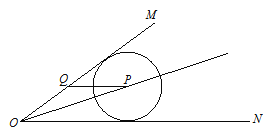
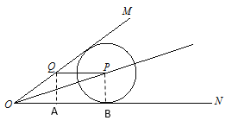
【题目】如图,∠MON=30°,p是∠MON的角平分线,PQ平行ON交OM于点Q,以P为圆心半径为4的圆ON相切,如果以Q为圆心半径为r的圆与![]() 相交,那么r的取值范围是( )
相交,那么r的取值范围是( )
A.4<r<12B.2<r<12C.4<r<8D.r>4
【答案】A
【解析】
过点Q作QA⊥AN于A,过点P作PB⊥ON于B,得到四边形ABPQ是矩形,QA=PB=4,根据∠MON=30°求出OQ=2QA=8,根据平行线的性质及角平分线的性质得到PQ=8,再分内切与外切两种求出半径r,即可得到两圆相交时的半径r的取值范围.
过点Q作QA⊥AN于A,过点P作PB⊥ON于B,
∵PQ∥ON,
∴PQ⊥PB,
∴∠QAB=∠QPB=∠PBA=90°,
∴四边形ABPQ是矩形,
∴QA=PB=4,
∵∠MON=30°,
∴OQ=2QA=8,
∵OP平分∠MON,PQ∥ON,
∴∠QOP=∠PON=∠QPO,
∴PQ=OQ=8,
当以Q为圆心半径为r的圆与![]() 相外切时,r=8-4=4,
相外切时,r=8-4=4,
当以Q为圆心半径为r的圆与![]() 相内切时,r=8+4=12,
相内切时,r=8+4=12,
∴以Q为圆心半径为r的圆与![]() 相交,4<r<12,
相交,4<r<12,
故选:A.

【题目】某区正在积极创建国家模范卫生城市,学校为了普及学生卫生健康知识,提高学生创卫意识,举办了创卫知识竞赛,以下是从初一、初二两个年级随机抽取20名同学的测试成绩进行调查分析,成绩如下:
初一:75 88 93 65 78 94 89 68 95 50 89 88 89 89 77 95 87 88 92 91
初二:74 96 96 89 97 74 69 76 72 78 99 72 97 85 98 74 89 73 98 74
(1)整理、描述数据:
成绩 |
|
|
|
|
|
初一(频数) | 1 | 2 | 3 |
| 6 |
初二(频数) | 0 | 1 | 9 | 3 | 7 |
(说明:成绩90分及以上为优秀,80~90分为良好,60~80分为合格,60分以下不合格)
分析数据:
平均数 | 中位数 | 众数 | |
初一 | 84 |
| 89 |
初二 | 84 | 81.5 |
|
请根据上述的数据,填空:![]() ______;
______;![]() ______;
______;![]() ______;
______;
(2)得出结论:
你认为哪个年级掌握创卫知识水平较好并说明理由.(至少从两个不同的角度说明推断的合理性).